说到爱的方程式,大家一定不陌生。
其中最著名的是笛卡尔的心形线 r=a(1−cosθ) 的故事,但这个是在极坐标系下的方程。在平面直角坐标系下,心形线的方程是 x2+y2+ax=ax2+y2(下图是 a=1 的情况)。
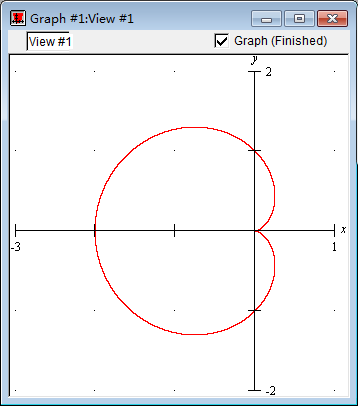
关于这个故事,读者可以自行了解。而本文讨论的是平面直角坐标系内的方程。
从椭圆开始
我们熟知,(焦点在 x 轴上的)椭圆的标准方程为
a2x2+b2y2=1
那么,如果焦点不在坐标轴上,椭圆方程又是什么样子的呢?
显然,只需要将标准椭圆旋转一定角度,再进行平移,就可以得到一切椭圆的方程了。
将椭圆平移是简单的,这里我们将问题简化,先考虑标准椭圆的旋转。
复数立大功
关于旋转,连接角度与长度的一大桥梁便是三角函数。而复数又与三角函数密切相关,这里我们处理的原理是复数乘法的几何意义——模相乘,辐角相加。
假设复平面上的点 P=x+yi 满足 a2x2+b2y2=1,那么将 P 逆时针旋转 θ 后得到的 P′ 满足
P′=P(cosθ+isinθ)=(xcosθ−ysinθ)+i(xsinθ+ycosθ)
假设 P′=x′+y′i,那么就有
{x′y′=xcosθ−ysinθ=xsinθ+ycosθ
于是解得
{xy=x′cosθ+y′sinθ=y′cosθ−x′sinθ
再将其代回标准方程化简:
a2x2+b2y2b2x2+a2y2b2(x′cosθ+y′sinθ)2+a2(y′cosθ−x′sinθ)2(b2cos2θ+a2sin2θ)x′2+(b2−a2)x′y′sin2θ+(a2cos2θ+b2sin2θ)y′2=1=a2b2=a2b2=a2b2
于是,我们就得到了椭圆 a2x2+b2y2=1 逆时针旋转 θ 后的方程:
(b2cos2θ+a2sin2θ)x2+(b2−a2)xysin2θ+(a2cos2θ+b2sin2θ)y2=a2b2
椭圆变爱心
为了计算简便,我们取 a=4,b=2,θ=4π,那么旋转后的方程就是
5x2−6xy+5y2=16
方程所表示的曲线长这样子:
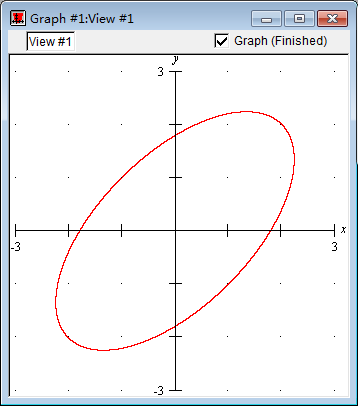
我们观察其在 y 轴右边的部分,它非常像爱心的一半,那么我们只需要让 y 轴左边的部分和右边的部分对称,就可以得到爱心方程。
既然爱心方程关于 y 轴对称,也就是说如果 (x,y) 满足方程,则 (−x,y) 也满足方程。
于是我们自然而然地想到——将方程中的 x 全部替换为 ∣x∣,那么方程就变成了:
5x2−6∣x∣y+5y2=16
那我们就做完了,这是它所表示的曲线:
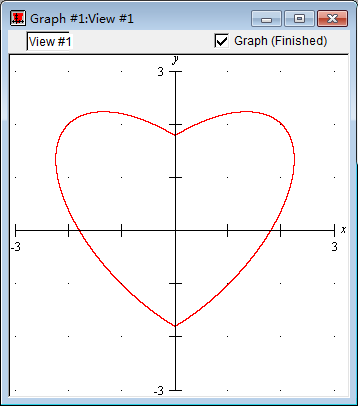
事实上,你可以对椭圆旋转不同的角度以得到不同的爱心方程,我这里为了方便计算只旋转了 4π。
填充颜色
如果我们要对爱心填充颜色,那么就需要将等号改成不等号。
先考虑椭圆的标准方程 a2x2+b2y2=1,如果 (x0,y0) 在椭圆内,设 (x0,y1) 在椭圆上,显然会有 ∣y0∣<∣y1∣,那么 a2x02+b2y02<a2x02+b2y12=1。
也就是说,在椭圆内的点组成的区域为 a2x2+b2y2<1。
依法炮制进行旋转,就得到旋转后椭圆内区域满足不等式
(b2cos2θ+a2sin2θ)x2+(b2−a2)xysin2θ+(a2cos2θ+b2sin2θ)y2<a2b2
于是我们的爱心区域满足不等式
5x2−6∣x∣y+5y2<16
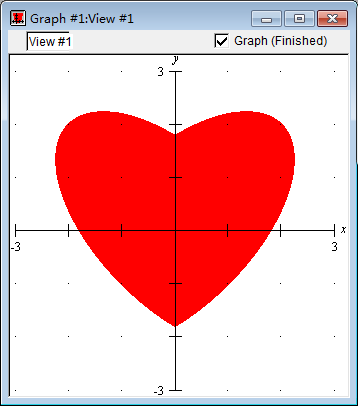
我心碎了
这部分原创于 Matrix67 的博客。
如果我们想要这颗心碎掉,那又该如何处理呢?
心碎的裂缝非常像是在 y 轴上的正弦曲线 x=siny。于是我们很自然地想到,只需要在不等号左边加上一个东西,这个东西在函数 x=siny 附近非常大,大到可以使不等式不成立,而在爱心的其他地方的值非常小,小到几乎不影响不等式,那么就达到了我们的目的。
很显然,函数 y=∣x∣k 可以满足我们的需求(其中 k 是常数,取决于我们从哪里开始函数值发生大幅度的变化)。
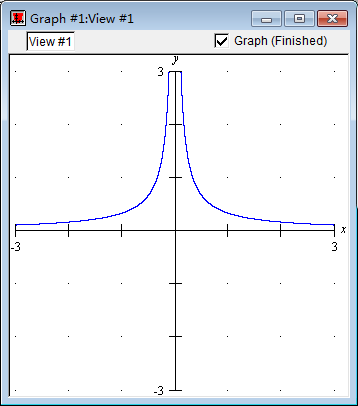
当然,你也可以使用 y=xnk,其中 n 为偶数,n 越大突变效果会更好。
哦对了,这个正弦曲线对于我们的爱心来说有点太大了,完全不像是裂缝:
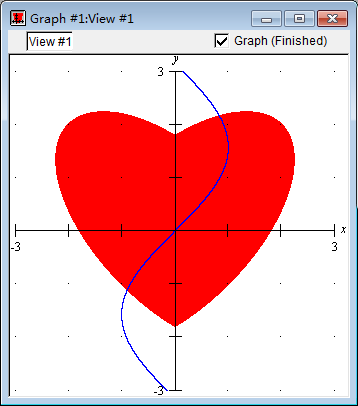
我们可以减小其振幅,增大其频率,使其真正像个裂缝。为了做到这件事,我们把 y 改成 5y,把 x 改成 5x。
另外,我们在等号的一边加上一个负号,以便后续处理。由恒等式 −sinθ=sin(−θ) 可以知道,这实际上只会将曲线对称一下,形状并没有改变。将所有项移到一边以后,我们可以得到
5x+sin5y=0
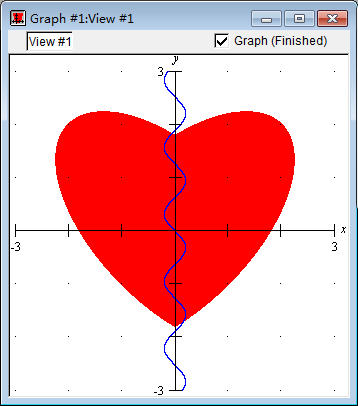
注意,当 ∣x∣ 越远离大时, ∣5x+sin5y∣ 就会越大,套入我们刚刚的 ∣x∣k,再加到我们爱心方程的左边,这里我取 k=5,便可以得到
5x2−6∣x∣y+5y2+∣5x+sin5y∣5<16
这个式子有点丑,我们移项乘分母变下形
(16+6∣x∣y−5x2−5y2)∣5x+sin5y∣>5
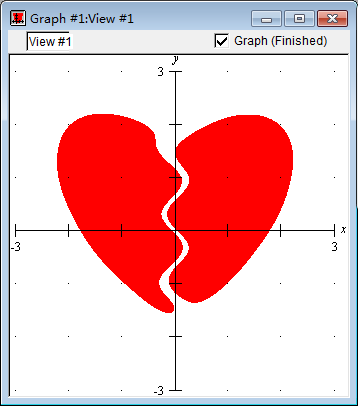
这便是我们想要的。
上文提到,可以使用 y=xnk 作为突变的函数,这里给出一个构造的方程,个人认为更加好看,读者可以自行探究(对了,当 n>4 后改变 k 和 n 的值对图像没有太大影响,因为取倒数之后实在是太大了):
(16+6∣x∣y−5x2−5y2)(5x+sin5y)4>1
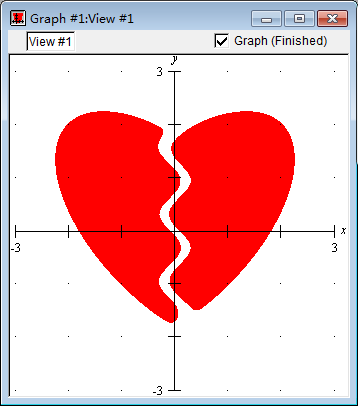
画图软件支持:GrafEq








