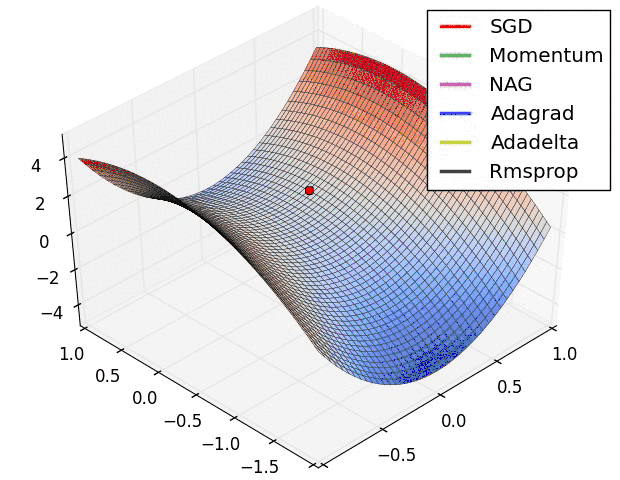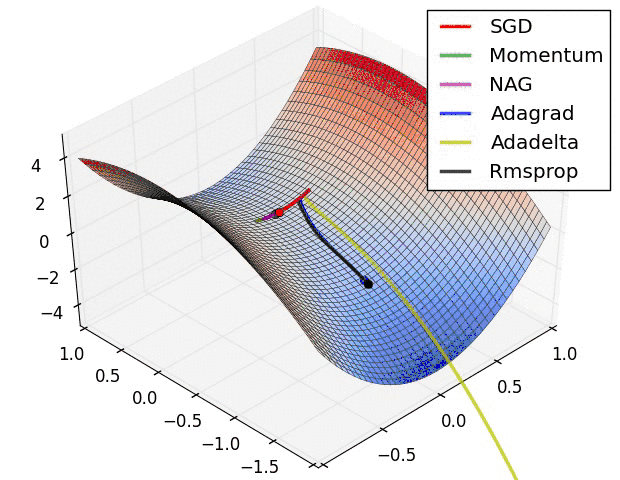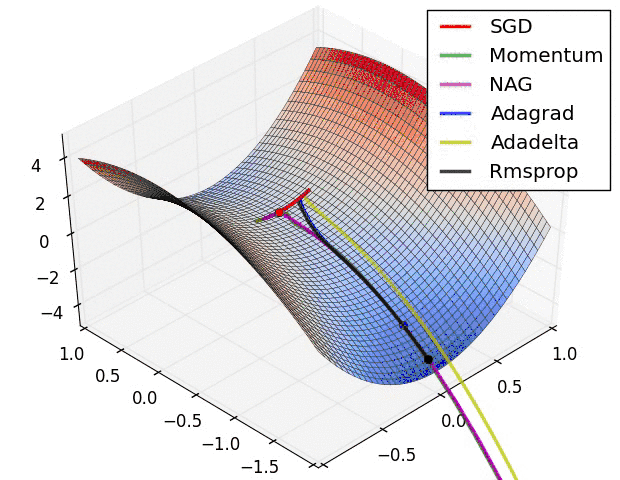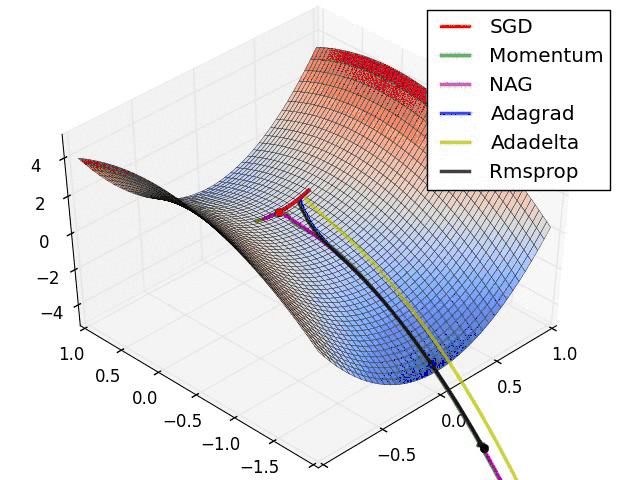
[科普] 浅谈梯度下降法

· 2019-10-04 ·

最近在搞手写数字的识别（好难啊QAQ）。

其中有个代码中重要的部分是梯度下降，这部分比较难理解，这里给大家介绍一下，顺便写一篇学习笔记吧。

Update 2025/02/18
阅前须知：梯度下降法（大概是）连一名中规中矩的人工智能专业本科学生都不会学习到的内容（因为现阶段本科人工智能专业课程设计得十分难评），作为鄙人刚上初二时写的一篇学习笔记（实际上从现在来看是一篇拙到不能再拙的拙文），这篇文章可能误导性极大且毫无专业性，并不适合用于学习来阅读，如果您坚持阅读，这可能浪费您人生中宝贵的十五分钟。

注意：本文所讲的梯度下降指的是批量梯度下降法（Batch gradient descent），简称BGD。

写在前面

为什么写这个

因为网上讲的过于深奥，对新手十分不友好（我用了差不多一个月才理解它，肯定是我太蒻了），目前我认为最好的文章就是这篇了。

另外，本文会用通俗简单的方式给大家呈现梯度下降法（因为要做到通俗，有时会把严谨忽略）。

梯度下降是什么，有什么用

度娘的解释：

梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。——百度百科

在 $3b1b$ 中的解释：

它（梯度下降法）不仅是神经网络学习的基础，机器学习中很多其他的技术也是基于这种方法。—— $3Blue1Brown$

别看这里有这么一堆东西，简单来说就是求一个多元函数的极值（最大值和最小值）。

这个算法在神经网络中是一个常用的算法。

什么是梯度下降

假如说，你在一座山上，需要尽快下山，但是此时浓雾很大，你看不到最低点，此时你的做法应该：

A. 看脚下周围哪边陡，一直往陡的方向走

B. 一直往一个方向走

C. 看脚下周围哪边缓，一直往缓的方向走

如果你有亲身经历的话，那么是选A，但大多数人应该是没有的，我来解析一下：

首先你如果只往一个方向走的话，只有很少的概率能成功下山，有时还会走上一条上山的路。因此排除B。

其次，因为你往陡的地方走一步，很明显比往缓的地方走一步下降得快。所以选A。

而梯度下降法就是这个原理，走最陡的路~~，做不同的自己~~。

另外，如果是上山，也是类似的思路，往陡的地方上山，也可以以最快的速度到达最高点。

理解梯度下降

首先，你需要一些前置知识：

数学函数和计算机函数（想必大家应该都是懂的，这里直接放一个链接）
导数（如果你还是不懂，请看下面，如果你懂，可以选择跳过）

导数是什么

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。——百度百科

对于加粗字，我举一个例子：

例如 $f(x)=2$ ，它的导数 $f'(x)=0$ ，下面用一张图来解释一下：

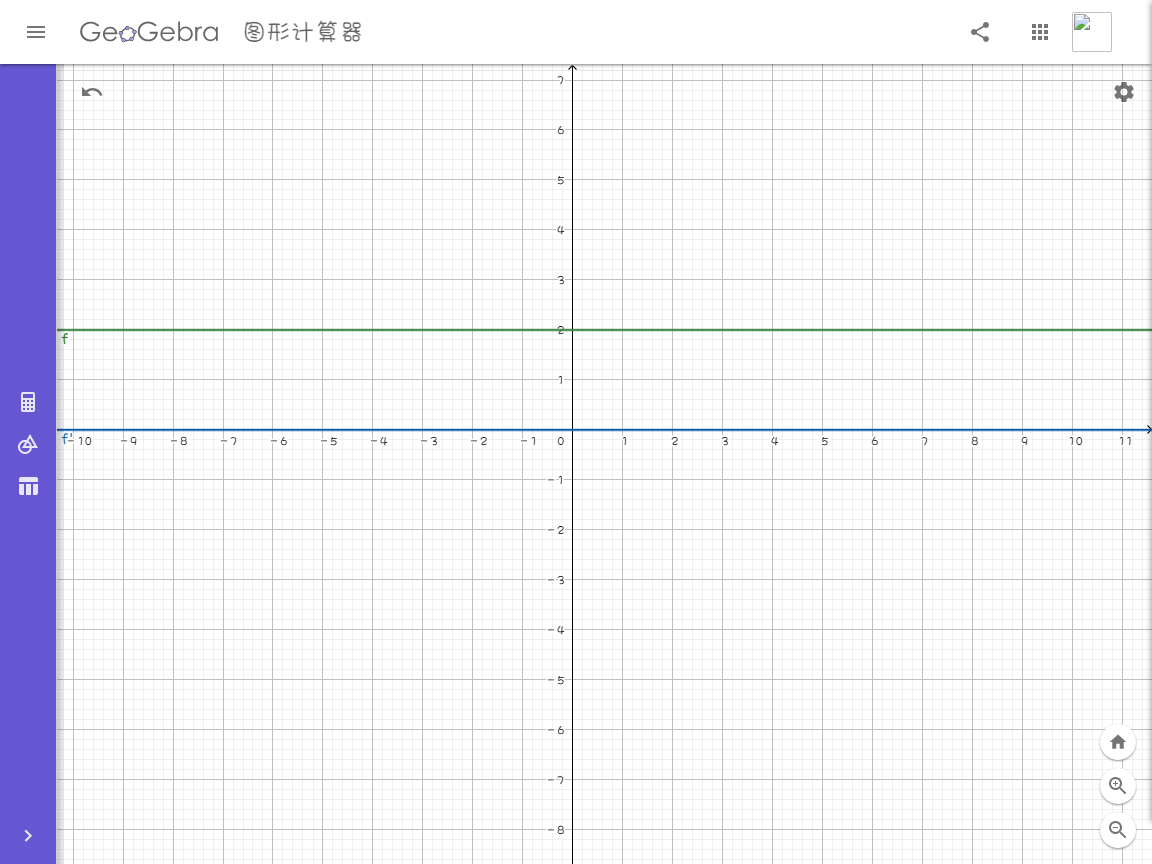
你会发现，对于 $f$ 函数的 $y$ 一直保持在 $2$ ，既没有变大，也没有变小，那么对于 $f'$ 就是一直保持在 $0$ （变大就会是正数，变小会是负数，如果不变就是 $0$ ）。我们再看下面这个例子：

$f(x)=x$ ，它的导数是 $f'(x)=1$ 。

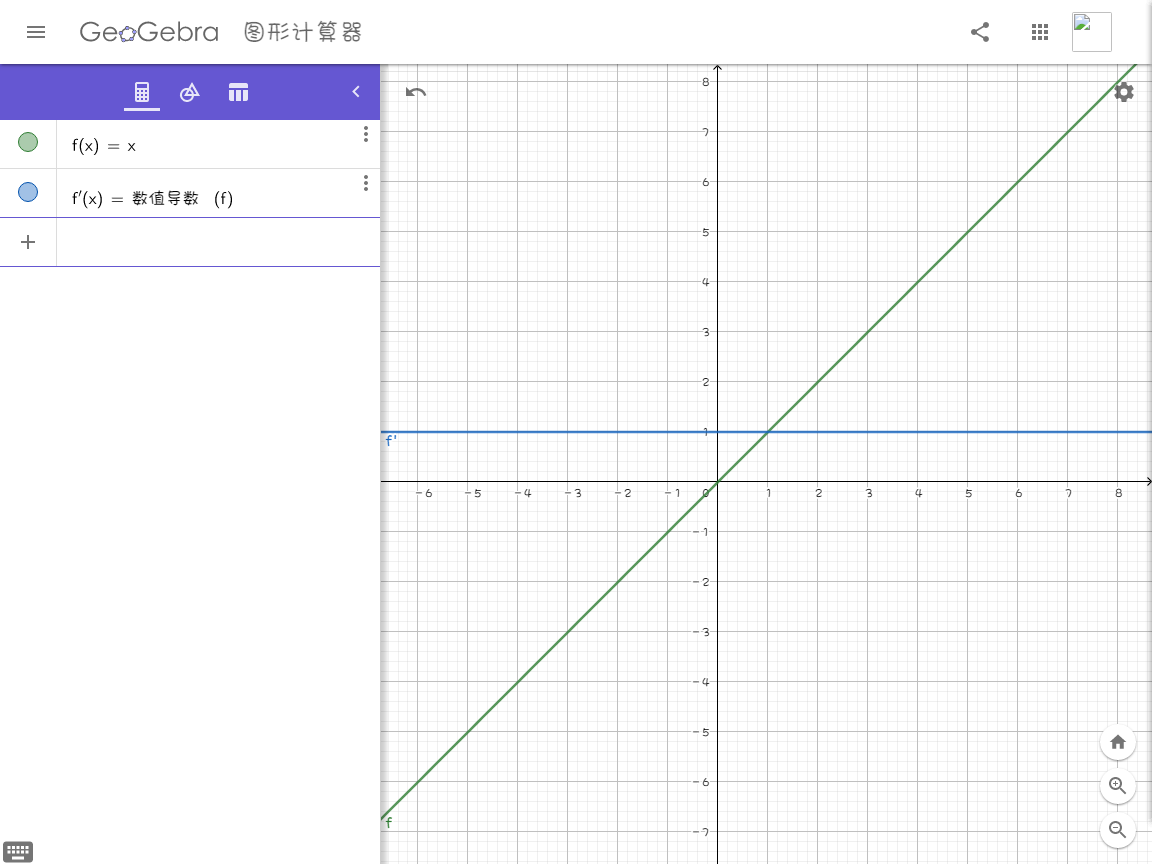
因为这条绿色的线是匀速增长的（每时每刻都以 $1$ 的速度增长），因此它的导数一定是直的，又因为 $f$ 的增长率是 $1$ ，因此它的导数都是 $1$ 。

这两个例子告诉我们：某一点的导数是这一点的增长率（变化率）。

另外，对于其他复杂函数，你需要用到导数表，或者说下面会讲到一个万能公式（他抛弃了恶心的导数表）。

但是，假如你不知道原函数，要怎么求某一个点的导数呢？

这时，我们需要用到函数的切线。

那，切线又是什么呢？

切线就是正好碰到曲线某一点的直线。如果在某一点作了切线，那么这个点就叫作这条切线的切点。

刚开始，我一直不能理解，某个点的切线为什么一定要长那样子，而且为什么可以一个点确定一条直线，但后来，我去找了电脑老师（没错你没听错），他通俗的用几句话把它给描述清楚了：

把曲线无限放大

那么该点左右范围内，极小极小极小的一小段圆弧

就应该是一条直线

延长这条直线，就是该点的切线

当然，这里我放了一张gif，方便大家理解：

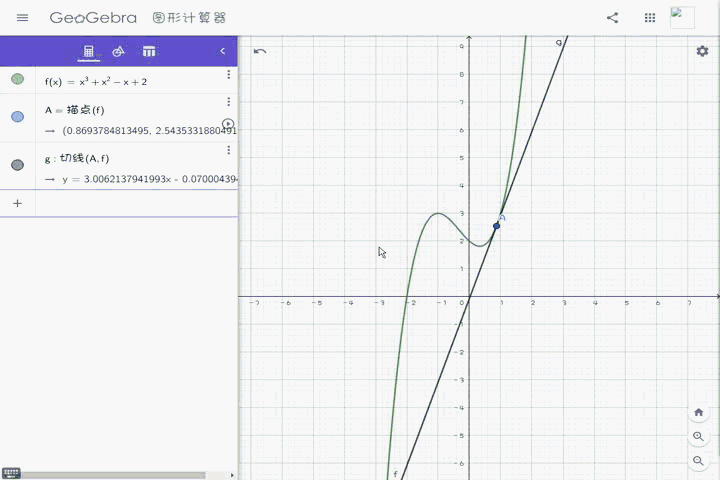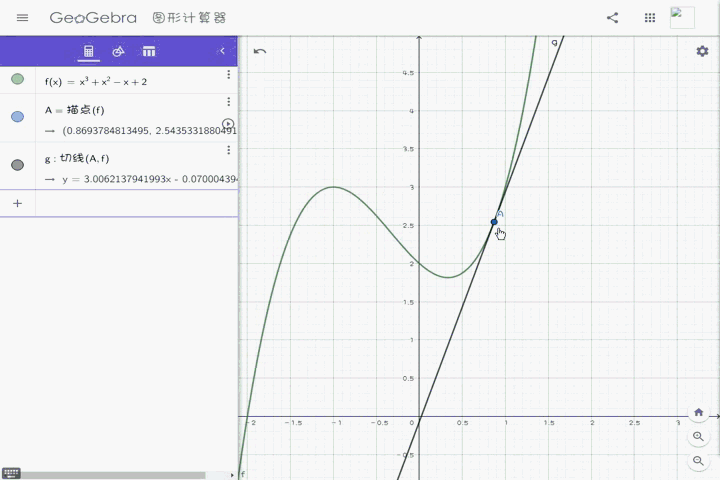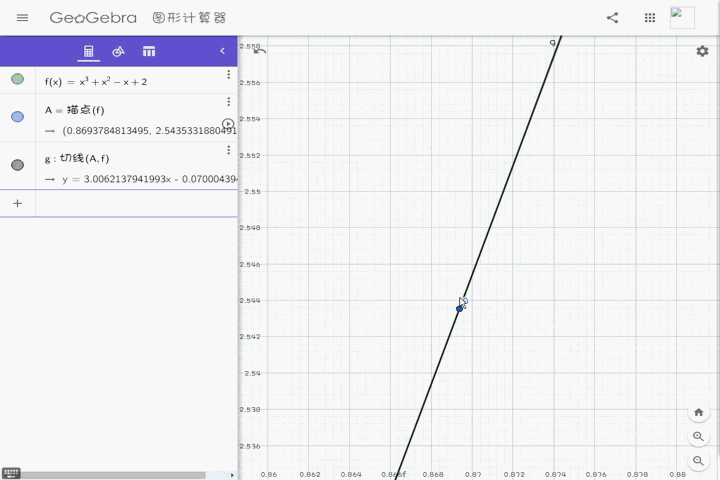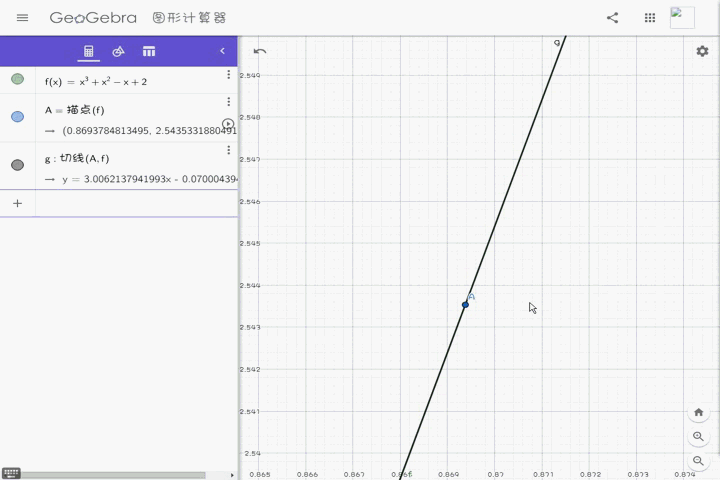
我这里虽然没有无限放大，但是在放大到一定时候，曲线就会近似于直线。

然后，我们知道切线是什么了，但是下一步要怎么做呢？

我可以告诉你：某点的切线的斜率就是该点的导数！（上面百度百科也有提到）

那什么是斜率呢？

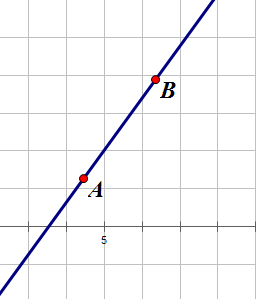
某一条直线的斜率就是对于横坐标倾斜程度的量，我们通常用一条公式来表示以两个点（假设我们这里是 $A$ 和 $B$ ）构成的直线的斜率 $k$ ：

k=\frac{y_B-y_A}{x_B-x_A}

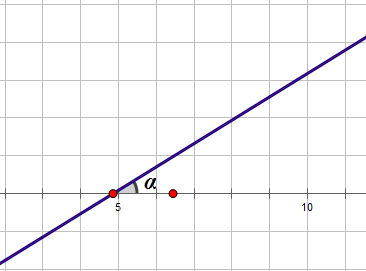
或者说是直线与横轴相交所形成的夹角的正切值：

k=\tan\alpha

东西有点多啊，我们把这几个概念组合起来成为一句话吧：

函数的某个点的切线是一条直线，这条切线的斜率就是这个函数在这个点的导数。

如果说只给你一个点 $a$ ，求函数 $f(x)$ 在这个点的导数，而且你并不知道 $f(x)$ 的表达式，用第二个公式会比较麻烦，相对来说第一个公式会比较简单。

但是，我们只有一个点啊！

没事，我们只需要取两个点，使他们十分接近，然后再计算他们所构成的直线的斜率，就可以了。

假如说两个点的横坐标的差是 $p$ ，那么套进式子：

k=\frac{y_B-y_A}{x_B-x_A}

k\approx\frac{f(a+p)-f(a)}{(a+p)-a}

k\approx\frac{f(a+p)-f(a)}{p}

当 $p$ 趋近于 $0$ ， $k$ 的值就会越精确，即 $k=\lim\limits_{p\to0}\frac{f(a+p)-f(a)}{p}$ 。

~~记住这个公式！这个公式可以抛弃求导，因此我叫它万能公式。~~

Update 2019.12.31
感谢@锦依卫Lijilai 大佬和@EMT__Mashiro 大佬指出的错误，应为抛弃导数表。

记住这个公式！这个公式可以抛弃导数表，因此我叫它万能公式。

梯度是什么

梯度的本意是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。——百度百科

向量又是个啥啊？

向量代表着一个方向，它具有方向和大小，或者说你可以当它是具有方向的线段。（就类似于你在 $QQ$ 截图里拉箭头那样）

梯度正好符合我们开头所讲的，使变化最快对应着下山要走最陡的地方变化才快。

记住，梯度是一个向量！~~（要考的）~~

开始理解梯度下降

这里是整个梯度下降的核心公式：

\large new=old-\alpha \nabla f(old)

主要意思是：新的坐标等于旧的坐标减去旧坐标的函数的梯度。

这就很符合上面我们所说的下山。你新的站立点是你旧的站立点减去你每步的长度乘上下山的方向。

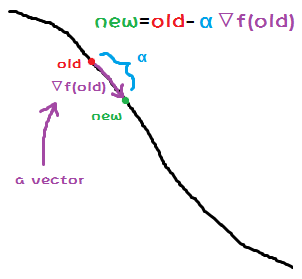
这图画的什么意思啊？别急，继续往下看。

只要一直计算 $new$ 的值，然后带进 $old$ 再算出 $new$ 的值，如此循环下去， $new$ 就会变成 $f$ 函数的最低点。

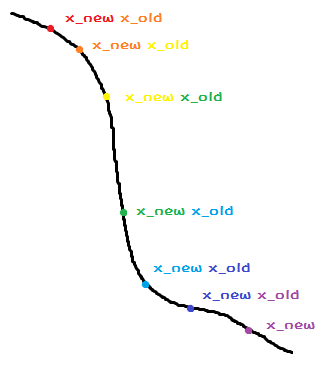
另外，在梯度下降刚开始时，我们可以随便找几个随机数作为初值，然后通过这些随机数去计算。

那里面的变量又代表什么意思呢？

$new$

这个 $new$ 代表着一个新的坐标，但他不一定是一个平面上的坐标，也不一定是三维空间里的坐标，它是一个在 $n$ 维空间里的坐标，其中，这个 $n$ 的值是由 $f$ 函数的参数个数来决定的。

$old$

上面是新坐标，那么这就是一个旧坐标了。它也是一个在 $n$ 维空间里的坐标， $n$ 的值也是由 $f$ 函数的参数个数确定的。

$\alpha$

这是一个步长，或者说可以叫学习率，可以说是你下山的时候走一步的长度。它是控制下山的速度的，他必须不能太大，又不能太小，如果太大，你就会错过最低点（远离最优解），或者一直到达不了最低点；如果太小，你就会很久不能到达最低点（收敛慢）。

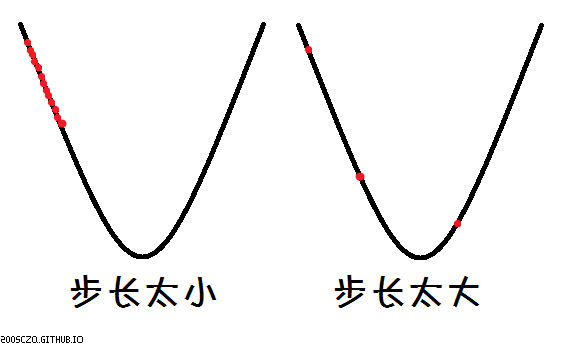
如果说 $\alpha$ 随下降次数而变小，那就更好了。

$\nabla f(old)$

$\nabla$ 是梯度的意思，要记住这是一个向量， $\nabla f(old)$ 代表 $f$ 的梯度，而 $-\nabla f(old)$ 是负梯度的意思，意味着我们需要下降。

如果我们要上升，就是 $+\nabla f(old)$ 。

然后，怎么求 $\nabla f(old)$ 呢？

你需要先知道定义， $\nabla f(a_1,a_2,\dots,a_n)=(\frac{\partial f}{\partial a_1},\frac{\partial f}{\partial a_2},\dots,\frac{\partial f}{\partial a_n})$ 。

然后，你肯定会说：这 $\frac{\partial f}{\partial a_1}$ 又是个啥啊？

$\frac{\partial f}{\partial a_1}$ 是函数 $f$ 对变量 $a_1$ 的偏导数。

偏导数又是啥？

偏导数指把某个函数里非某个变量的其他变量当做常数，然后再对这个函数求导。

它表示为 $\frac{\partial \text{函数}}{\partial \text{变量}}$ 。例如
$\frac{\partial f}{\partial a_1}$ 意味着，把函数 $f$ 里的其他变量（除 $a_1$ 外的变量）当做常数，然后再对函数求导。

如果你还不能明白，我再举一个例子：

假如有这么一个函数：

f(x,y,z)=x^2+5xy+z^3

所以：

\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}(x^2)+\frac{\partial}{\partial x}(5xy)+\frac{\partial}{\partial x}(z^3)

此时 $x^2$ 的导数是 $2x$ ； $y$ 是常数，通过公式 $f(x)=Cx,f'(x)=C$ 可以得出 $\frac{\partial}{\partial x}(5xy)=5y$ ； $z^3$ 是常数，常数的导数是 $0$ 。

所以得出：

\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}(x^2)+\frac{\partial}{\partial x}(5xy)+\frac{\partial}{\partial x}(z^3)=2x+5y+0=2x+5y

同理可得：

\frac{\partial f}{\partial y}=\frac{\partial}{\partial y}(x^2)+\frac{\partial}{\partial y}(5xy)+\frac{\partial}{\partial y}(z^3)=0+5x+0=5x

\frac{\partial f}{\partial z}=\frac{\partial}{\partial z}(x^2)+\frac{\partial}{\partial z}(5xy)+\frac{\partial}{\partial z}(z^3)=0+0+3z^2=3z^2

所以

\nabla f(x,y,z)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})=(2x+5y,5x,3z^2)

实战问题

让我们来做几道练习题：

入门难度

使用梯度下降法求 $x^2$ 最小时的 $x$ 值。

首先已知：

f(x)=x^2

所以：

\nabla f(x)=\frac{\partial f}{\partial x}=2x

假如我们这里 $\alpha=0.4$ ，那么公式 $new=old-\alpha \nabla f(old)$ 变成 $x_{new}=x_{old}-0.4\times2x_{old}$ 。

初始值为 $x=10$ 。（可以是其他）

$x_0=10-0.8\times10=2$ $x_1=x_0-0.8\times x_0=0.4$ $x_2=x_1-0.8\times x_1=0.08$ $\dots$ $x_{20}=x_{19}-0.8\times x_{19}=2.1\times10^{-14}$

当迭代次数越多， $x$ 就会趋近于 $0$ 。

因此我们得知，最小值是 $x=0$ 。

但是这个很明显可以看出来，下面我们来试两个变量时的情况。

普及+/提高

使用梯度下降法求 $x^2+(y-1)^2+1$ 最小时的 $x,y$ 值。

已知：

f(x,y)=x^2+(y-1)^2+1

所以：

\frac{\partial f}{\partial x}=2x

\frac{\partial f}{\partial y}=2(y-1)

所以：

\nabla f(x,y)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})=(2x,2(y-1))

然后，要怎么相减呢？

其实很简单，例如 $(1,2)-(1.2,0.5)$ 就是分别相减，即 $(1-1.2,2-0.5)=(-0.2,1.5)$ 。

那么，开始计算了。（ $\alpha=0.2,(x,y)=(10,10)$ ）

由于我太懒了，直接贴代码吧：

C++代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
	double x=10,y=10,st=0.2;//初始化
	for(int i=0;i<51;i++){//随便迭代个51次
		x=x-st*2*x;//核心
		y=y-st*2*(y-1);//核心
		printf("%.10lf %.10lf\n",x,y);
	}
}

最后 $(x,y)$ 会趋近于 $(0,1)$ 。

但是这并没有体现到梯度下降法的强大，因为只要你知道原函数，你一般都可以推导出最小值，来，我们来看一下终极之题。

NOI/NOI+/CTSC

已知 $f(x)$ ，用梯度下降法求 $f(x)$ 在最低点的 $x$ 值。

你可能会说：它连原函数表达式都不给我，怎么做啊（翻盘）？

还记得我们在上面讲导数的时候提到过：

假如你不知道原函数，要怎么求某一个点的导数呢？

而我们用的方法是求切线斜率。

那时，我们推导出一个万能公式：

f'(a)\approx\frac{f(a+p)-f(a)}{p}

其中 $p$ 是一个常数，越趋近于 $0$ 越好。

于是，

\nabla f(x)=\frac{\partial f}{\partial x}=f'(x)\approx\frac{f(x+p)-f(x)}{p}

所以我们计算 $\large x_{new}=x_{old}-\alpha\frac{f(x_{old}+p)-f(x_{old})}{p}$ 即可。

伪代码（没有 $f(x)$ ）：

#include<bits/stdc++.h>
using namespace std;
int main(){
	double x=10,st=0.2,p=1e-5;//初始化
	for(int i=0;i<51;i++){
		x=x-st*(f(x+p)-f(x))/p;//套入公式
		printf("%.10lf\n",x);
	}
}

这样做的好处有什么？

对所有函数通用，无需求导数，只要它能给你返回函数值，无论是返回 $\sqrt{n}$ 还是地球在赤道和经度 $n^\circ$ 的海平面高度（这个不能推导出函数表达式），它都可以解决。

但是也有一个不足的地方，可能会有误差。

另外，如果 $f$ 里的变量多起来，或者调用一次 $f$ 函数比较耗时的话，速度会降低。（神经网络就是这样，变量又多，调用又耗时）

同时，如果有多个变量，也是一样的，只要将代码中的：

x=x-st*(f(x+p)-f(x))/p;

变成

x1=x1-st*(f(x1+p,x2,x3,...,xn)-f(x1,x2,x3,...,xn))/p;
x2=x2-st*(f(x1,x2+p,x3,...,xn)-f(x1,x2,x3,...,xn))/p;
x3=x3-st*(f(x1,x2,x3+p,...,xn)-f(x1,x2,x3,...,xn))/p;
...
xn=xn-st*(f(x1,x2,x3,...,xn+p)-f(x1,x2,x3,...,xn))/p;

即可。

什么？你说你是 $P$ 党？看不懂 $C++$ 代码？

那我就用数学符号表示吧（前方高能）：

例如有一个多个变量的函数 $f(x,y,z)$ ，那么：

\nabla f(x,y,z)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})

=\lim\limits_{p\to0}(\frac{f(x+p,y,z)-f(x,y,z)}{p},\frac{f(x,y+p,z)-f(x,y,z)}{p},\frac{f(x,y,z+p)-f(x,y,z)}{p})

有没有一种要晕了的感觉？

总结

重温一下

梯度下降是求一个多元函数的极值（最大值和最小值）的算法。

它对于所有可求导函数都适用。

核心公式：

\large new=old-\alpha \nabla f(old)

主要步骤：

对原函数求导。
设定初值 $a_1,a_2\dots$ （以函数参数个数决定），学习率 $\alpha$ （和切线斜率精度 $p$ ，如果你能对函数求导，那就不需要设置这个了）。
设置迭代次数 $i$ 。
开始下降（套入核心公式）。

最后讲一下时间复杂度： $O(nm)$ （ $n$ 指函数的变量个数， $m$ 指的是迭代次数）

如果是上面的那个“万能方法”，则可能会更耗时一点，具体看函数调用一次的时间。

空间复杂度 $O(n)$ （ $n$ 指函数的变量个数）。

优点：

迭代次数少。（因为走的方向很精准）
总能达到最优解，若为凸函数，保证得到最优解。

缺点：

计算量大。（每次下降的时间是 $O(n)$ ）
有点耗内存。
不同的初值可能会得到不同的结果。（凸函数除外）

拓展

因为 $BGD$ 需要计算所有变量的导数，因此速度会比较慢。

所以人们想出了一个想法：

每次只计算一个变量的导数，然后把迭代次数大大增加，至于是哪个变量可以用随机数或者循环。

那么时间复杂度就变成 $O(m)$ 。

这个算法叫做随机梯度下降法（Stochastic Gradient Descent），简称 $SGD$ 。

尽管 $SGD$ 的迭代次数比 $BGD$ 大很多，但一次迭代的时间非常快。

限于篇幅问题，这里不展开细说，原理与 $BGD$ 是相似的。

它的优点有：

速度要比 $BGD$ 快得多
好像没有了

缺点：

迭代次数多
容易卡 $bug$ ，例如卡在函数的鞍点（即一个方向看这个点是最小值，另一个方向看是最大值，如下图，只看红色的线）

（图源此处）