周三上奥数课,惨遭滑铁卢。
注意:本文为方便阅读,定义 ϕ=21+5。
发现问题
奥数课数学老师不在,让我和 RioBlu 来讲题,最后剩一段空余时间,我心血来潮要表演一个魔术:
“在这十个格子中,在前两个格子各填上一个正整数。当然,不要告诉我。让从第三个格子开始填,每个格子里的数是前两个格子的和,填到第九个格子为止。把第九个格子的数告诉我,我就可以告诉你第十个格子里的数。”

一通操作猛如虎,我将第十个格子算出了 2239,正确答案却是…

了解问题
秘诀
假设第九个格子的数字为 n,那么第十个格子的数字就是 ⌊ϕn+21⌋(其中 ⌊x⌋ 代表将 x 向下取整)。
通俗点说,把第九个格子的数乘上 ϕ,再四舍五入,就是第十个格子里的数了。
例如我填了 2 和 4,那么前九个格子应该是这样的:

然后你把第九个格子的数字,也就是 110 告诉我,我可以立马得出第十个格子的数是 110×ϕ≈178,而事实真的是这样,68+110=178:

原理
如果我们假设第一个格子为 a,第二个格子是 b,那么第九个格子和第十个格子的值我们就已经确定了:

如果将第九个格子乘上 ϕ,那么可以算出 (13a+21b)×ϕ≈21a+34b,这正好是第十个格子的值。
分析问题
事实上,这种方法只能得到一个近似的值,如果这个估算值与真实值不相等,那么就会失误。因此,要保证万无一失,估算值与真实值必须相等:
⌊ϕ(13a+21b)+21⌋=21a+34b
拿到这个方程的时候,我人都傻了,这种方程怎么解啊?
最后,我将它的函数图像画了出来,并花了两天时间找出了规律:
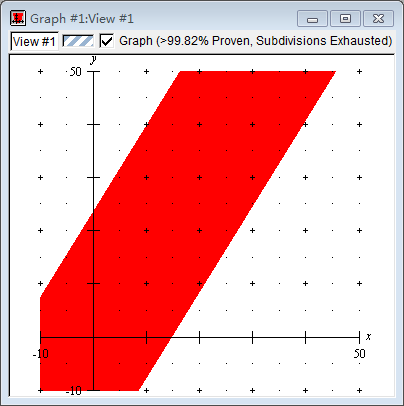
ϕa−k<b<ϕa+k(k=∣∣∣∣21(5−1)−13×21∣∣∣∣)
因此,在课上的例子中 a=100,b=4,将 a 代入上面的规律中可以算出 138.3<b<185.2,然而 4 并不在这个范围内,所以估算值与真实值不相等。
解决问题
那么,我们要怎么避免出现这种尴尬情况呢?
一方面,我们可以算更多的格子。
事实上,相邻两个格子之间的比值会趋近于 ϕ。通过观察上面的图我们发现,如果让对方填入前 n(n≤3) 个格子,并将第 n 个格子的值告诉你,那么这个值为 Fn−2⋅a+Fn−1⋅b。其中 Fn 为斐波那契数列的第 n 项。斐波那契数列就是前两个数为 1,从第三项开始每一项是前两项的和的数列,它长这样:{1,1,2,3,5,8,13,21,…}。
因此方程变成:
⌊ϕ(Fn−2⋅a+Fn−1⋅b)+21⌋=Fn−1⋅a+Fn⋅b
那么模仿上面的规律,你可以先给对方规定 a 和 b 的范围:
ϕa−k<b<ϕa+k(k=∣∣∣∣Fn−1(5−1)−Fn−2×21∣∣∣∣)
由于计算斐波那契数非常繁琐,因此利用斐波那契数列通项公式将 k 化简一下得到:
ϕa−k<b<ϕa+k(k=2ϕn−1)
然而,这还需要对方通过复杂计算自己的数字是否符合要求,魔术的气息瞬间就没了。因此另一方面,我们可以同时给 a 和 b 找一个范围,保证这个范围内的数绝对不会出错。
我结合函数图像的规律,舍大取小,得到 n 对应的最大范围:
0<a,b<2ϕn−2
这样,你就可以在表演之前先计算好这个数字,然后在表演时让对方保证两个数字不超过这个范围。这样,既避免了失误,又保证了魔术的说服力。
你能表演一下吗?

(首先约定填到第九个格子,计算 2ϕ9−2≈14.52,因此范围为 0<a,b<14.52)
“来,你随便想两个不超过 14 的正整数,填在前两个格子,不要给我看到。”

(ta 填入14 和 6。当然,你看不到 ta 填了什么)
“填好了吗?然后从第三个格子到第九个格子,每个格子都是前两个格子的和,把它们也填进去。”

(如上)
“你的第九个格子是多少?”
“308。”
(计算 308⋅ϕ≈498)
“第十个格子是 498。”
“哇好厉害,你怎么知道的?!”








