[科普] 如何找单峰函数的峰值
找单峰函数的峰值有什么用? 怎么找单峰函数的峰值?
别急,让这篇文章来告诉你.
Update 8/9/2025: 重新润色和排版了整篇文章,对部分图片进行重绘.
什么是单峰函数?
肯定要先听听度娘的解释啦:
单峰函数是在所考虑的区间中只有一个严格局部极大值(峰值)的实值函数.
如果函数 在区间 上只有唯一的最大值点 ,而:
- 在最大值点 的左侧,函数单调增加;
- 在点 的右侧,函数单调减少.
则称这个函数为区间 上的单峰函数.
就是函数的右侧单调下降,左侧单调上升,也可以这样解释:
为什么要找峰值?
-
摘自 Matrix67 的漫话二分(下):
生活中的很多东西都是这样,大了也不好,小了也不好,不多不少的时候最好。我最喜欢举的例子是,粉笔短了不好写且用得快,粉笔长了又容易断;为了贯彻拿 MM 打比方的精神,这里可以再举一些例子来说明这一情况的普遍性:陪 MM 出去玩的次数多了很快会腻,陪 MM 次数少了又会疏远;把握火候贯彻“半糖主义”方针是非常重要的。事实上,从硬盘缓存的大小到初期农民的个数,从每学期的学分到论文的长度,生活中几乎所有东西都是这样,就连饭量和睡眠时间也是。这些例子说穿了就是一个单峰函数,我们需要用尽可能少的试验次数快速找到极大点。永远不要以为决策者们面对的都是高中数学考卷上的“每涨 10 块钱就会少 100 个消费者”一类的屁话,这些屁话都是用来编二次函数题目的。现实生活中企业做决策时,样点实验、不断取舍、逐步逼近最优点仍然是最实在最有效的手段。
-
奥数填空题.
怎么找峰值?
本节中以 作为单峰函数在代码中呈现,并定义
其峰值为 .
#define f(x) pow(x,1.0/x)
const int pre=7; // pre为精度
double l=0,r=10,p=pow(10,-pre); // p为误差限
暴力枚举
最普通的方法肯定是暴力,设置步长,从左到右扫记录最大值.
| 条目 | 内容 |
|---|---|
| 优点 | 相对稳定 |
| 缺点 | 耗时长,精度低 |
| 时间复杂度 |
double maxx=-1;
for(double i=l+p;i<=r;i+=p) // 由于使用x^(1/x)为f函数,所以i不能为0
maxx=max(maxx,f(i)); // 寻找最大值
cout<<fixed<<setprecision(pre)<<maxx<<endl;
三分查找及其变体
不稳定的三分查找
像这种带有单调性的函数,让人不由自主的想起二分.
但是我们不能只取一个点,因为这是无法得出峰值在哪里的,所以我们需要取两个点,通过比较这两个点来得出峰值的位置.
阮大佬曾在他的博客中介绍了三分查找,主要是分一半再分一半的思想:
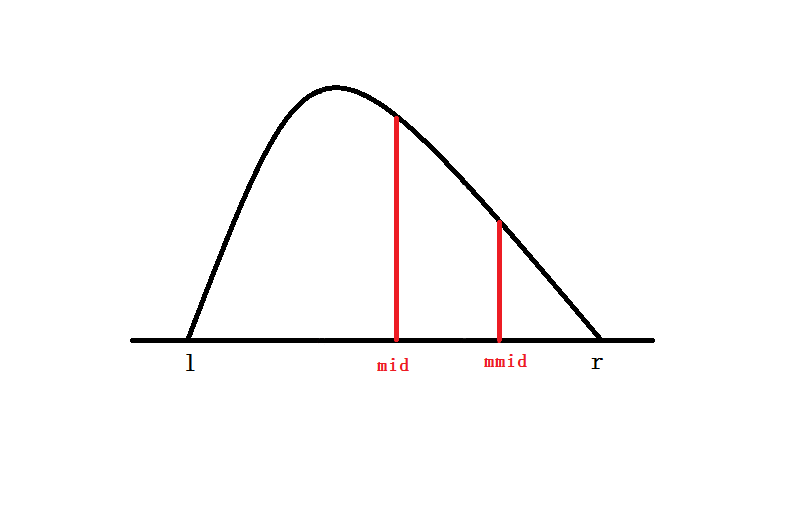
取 ,再取 . 比较 和 的值:
- 当 时,此时峰值必在 左侧,故更新 .
- 当 时,此时峰值必在 右侧,故更新 .
证明在链接里有,这里就照着我的思路再讲一遍吧(其实是差不多的):
当 时,若峰值在 右侧,会导致有两个峰,否则 不会大于,故峰值必在 左侧. 同样可以证第二个.
既然这样,我们就可以进行三分,每次可以舍去原长度的 或 .
另外,在原文里有提及到写法,一种是控制迭代次数,一种是直接控制精度,接下来的代码均以直接控制精度为例.
| 条目 | 内容 |
|---|---|
| 优点 | 速度快 |
| 缺点 | 不稳定 |
| 时间复杂度 | 最优 ,最劣 |
while(r-l>p){
double m1=l+(r-l)/2,m2=m1+(r-m1)/2;
// 先计算区间长度再进行加减的优点是不容易溢出
// 如果确保不会溢出,使用定比分点公式也可以
if(f(m1)<f(m2))l=m1; // 小于时舍去左边
else r=m2; // 舍去右边
}
cout<<fixed<<setprecision(pre)<<max(f(l),f(r))<<endl;
稳定的三分查找
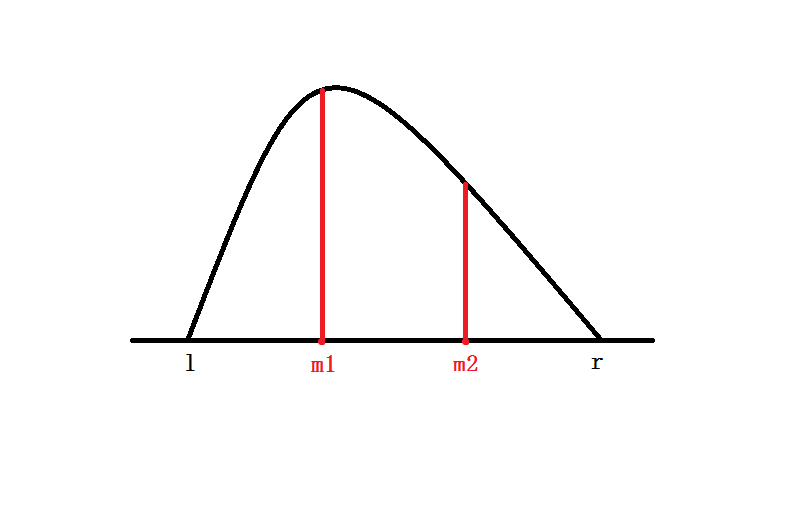
为了让算法变得更稳定,我们可以把这两个点设在三等分处,这样每次都一定会舍弃原长度的 .
| 条目 | 内容 |
|---|---|
| 优点 | 速度快,相对更稳定 |
| 缺点 | / |
| 时间复杂度 |
while(r-l>p){
double d=(r-l)/3,m1=l+d,m2=r-d; // 同样出于溢出的考虑
if(f(m1)<f(m2))l=m1;
else r=m2;
}
cout<<fixed<<setprecision(pre)<<max(f(l),f(r))<<endl;
类二分查找
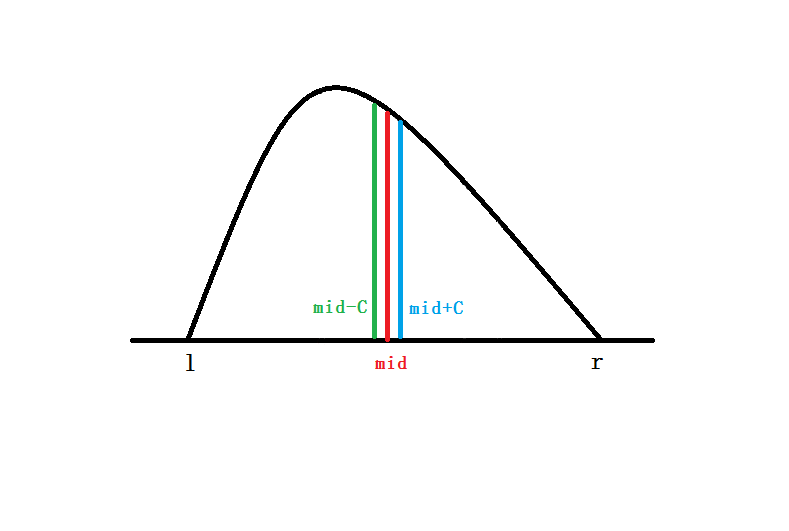
如果我们想需要速度更快,应该怎么处理呢?很容易可以想到,如果我们把 和 取得接近于中点,那么一次比较就可以舍去几乎的长度了!
所以我们可以考虑取中点 ,然后比较 和 ,其中 是一个很小的正数.
但是注意,如果 太小,那么浮点误差会导致计算得到 ,然后结束循环,最终你只会得到 .
| 条目 | 内容 |
|---|---|
| 优点 | 速度比普通三分快 |
| 缺点 | 浮点误差会导致比较失败 |
| 时间复杂度 |
while(r-l>=p){
double m=l+(r-l)/2; // 取中点
if(f(m-p)<f(m+p))l=m;
else r=m;
}
cout<<fixed<<setprecision(pre)<<max(f(l),f(r));
小瑕疵
上述三分法及其变体存在一些小瑕疵,当取得的两个点的函数值相同时,峰值在哪一侧均有可能:
- 峰值在左侧的点的左侧,此时两点之间所有函数值相等,同理有峰值再右侧的点的右侧.
- 峰值在两点之间,只是恰好取的两点函数值相等.
幸运的是,在现实生活和问题中,我们常常遇到的是下面的情况,故无需过多理会.
求导后二分查找
我们知道,函数峰值处导数为 . 因为是单峰,所以可以先对原函数求导,然后找 和 之间使 的值. 此时问题就转化成了二分查找(或牛顿迭代法等函数求零点算法).
问题就在于复杂的函数(以及多层复合的函数)很难求导. 而且在本例中 ,求完导后直接就能解得 .
在数学上直接就得到答案了,何必再用算法进行迭代?
实际上,由于一些超越方程不可在数学上解得,并且五次及以上的多项式方程无根式解,所以对于一些复杂的函数或高次的多项式方程而言,该方法展现出了一些独特优势.
| 条目 | 内容 |
|---|---|
| 优点 | 速度快 |
| 缺点 | 复杂函数难以求导,注意判断驻点 |
| 时间复杂度 | (未包含求导所需时间) |
正如上面所说,本例没有必要使用求导二分的方法求解,故此处以P3382 【模板】三分法为例,直接给出小黑AWM大佬的题解.
#include<cstdio>
using namespace std;
int n;
double a[20],L,R,k;
double f(double x){
double ans=0;
for(int i=n;i>=1;i--) ans=ans*x+a[i]; // 常数项没了
return ans;
}
int main(){
scanf("%d%lf%lf",&n,&L,&R);
for(int i=n;i>=0;i--)scanf("%lf",&a[i]),a[i]*=i; // a[i]*=i求导
while(R-L>=1e-6){ // 二分
double mid=(R+L)/2;
f(mid)>0?L=mid:R=mid; // 等价于if(f(mid)>0)L=mid;else R=mid;
}
printf("%.5lf\n",L);
return 0;
}
代码中使用了秦九韶算法重新调整了计算顺序:
将原本的 次乘法和 次加法化简为了 次乘法和 次加法.
// 普通算法
int f(int x){
int ans=0;
for(int i=0;i<=n;i++)
ans+=a[i]*pow(x,i);
return ans;
}
// 秦九韶算法
int f(int x){
int ans=a[n];
for(int i=n-1;i>=0;i--)ans=ans*x+a[i];
return ans;
}
0.618法
除了求导二分这个比较特殊的算法外,上面提到的三分查找及其变体最大的缺点其实是每次比较都要进行两次函数值的计算.
假如有这么一种做法,通过循环利用上一次比较时剩下的点. 使一个点被去掉后另一个点正好是下一次比较的其中一个点. 那么这两个点应该满足一些性质.
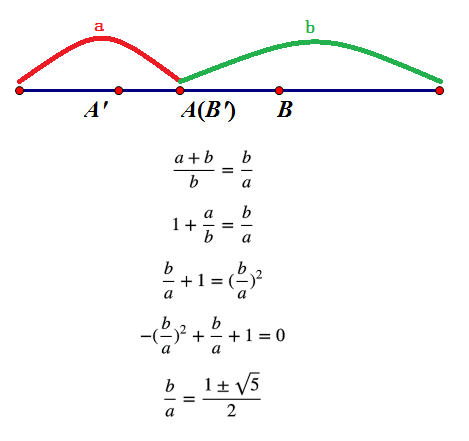
如上图,假如第一次比较在原线段上对称的两个点 和 ,不妨假设去掉了 右侧的部分.
那么下一次就可以仅需新增一个 ,并重复利用原先的 作为 进行比较.
可以发现一段相同的比例关系:
由于 ,设 将 分为左右长为 和 的两段,则
这样,我们就确定了两个点的位置了. 这个比例大家一定不陌生,这是著名的黄金分割率.
| 条目 | 内容 |
|---|---|
| 优点 | 重复利用已经计算过的点,速度极快 |
| 缺点 | / |
| 时间复杂度 |
#define F 0.38196601125010515179541316563436 // 较短的部分所占的比例
double d=F*(r-l),m1=l+d,m2=r-d;
double fm1=f(m1),fm2=f(m2);
while(r-l>p){
if(fm1>fm2){ // 舍去右边
r=m2;
m2=m1;
fm2=fm1; // 复用计算结果
m1=l+F*(r-l);
fm1=f(m1);
}else{
l=m1;
m1=m2;
fm1=fm2;
m2=r-F*(r-l);
fm2=f(m2);
}
}
cout<<fixed<<setprecision(pre)<<max(f(l),f(r))<<endl;
本节小结
一般的三分题,其实只有几个关键步骤:
- 选择要三分的函数和自变量.
- 设置好左端点和右端点.
- 调整精度.
最后套模板就可以轻松 AC.
复杂度比较
可以看到除了暴力之外,上述其他方法基本是 量级的,而优选法由于每次可以少计算一个点,进而在常数上获得优势:
| 方法 | 时的常数 | 的数值 |
|---|---|---|
| 不稳定的三分查找 | ||
| 稳定的三分查找 | ||
| 类二分查找 | ||
| 求导后二分查找 | ||
| 0.618法 |
如果说函数比较方便求导,首选求导二分,毕竟只需要 的时间,但同时需要注意求导所需的时间复杂度.
其他方法
直接看P3382的题解你就会发现有很多大法:
感兴趣的读者请自行了解,顺便膜拜以上这些大佬.
例题
给定一张边长为 的正方形纸,在四个角落各剪一个边长为 的小正方形,拼成一个无盖长方体,请输出这个长方体体积最大时的体积、高和底面边长(保留 5 位小数).
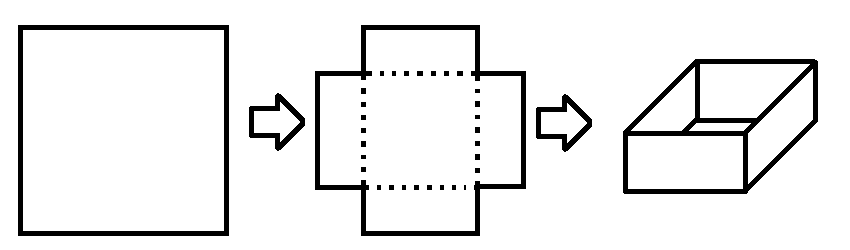
我们知道,长方体的体积 ,并且可以知道在 之间,体积先变大后变小.
所以可以对 的长度(即盒子的高)进行三分查找.
#include<bits/stdc++.h>
using namespace std;
double n;
double f(double x){ // 定义体积函数
return 4*x*(n-x)*(n-x);
}
int main(){
cin>>n;
double l=0,r=n;
while(r-l>1e-5){
double d=(r-l)/3,m1=l+d,m2=r-d;
double fm1=f(m1),fm2=f(m2);
if(fm1-fm2>=0)r=m2;
if(fm1-fm2<=0)l=m1;
}
cout<<fixed<<setprecision(5);
cout<<f(l)<<" "<<l<<" "<<sqrt(f(l)/l)<<endl; // a*a*h=f(h)
return 0;
}
当然,最快的还是求导:
所以就有正解求导做法:
#include<bits/stdc++.h>
using namespace std;
int main(){
double n;cin>>n;
cout<<fixed<<setprecision(5);
cout<<16*n*n*n/27<<" "<<n/3<<" "<<4*n/3<<endl; // 直接套用公式
}
如果你想做更多三分题,戳我.
结束语
蒟蒻第一次写文章,可能还不够熟练,如果文章有什么问题欢迎各位大佬指正,如果有什么漏掉的也欢迎各位大佬补充!