前几天刚学圆，想到之前见过一个公式，叫做「婆罗摩笈多公式」，昨天花了点时间推导了一下，今天来讲讲吧。

海伦公式

海伦公式相信大家一定不陌生，如果你还不知道，那么请看：

三角形三边分别为 a,b,ca,b,c，则它的面积为 p(p−a)(p−b)(p−c)\sqrt{p(p-a)(p-b)(p-c)}。其中，pp 为三角形的半周长，即 p=a+b+c2p=\dfrac{a+b+c}{2}。

那么大家肯定想过，对于一个四边形，只知道它四条边的长度，会不会也有长得像这样的公式呢？

你错了！

实际上，三角形具有稳定性，但四边形并没有。因此只知道四边形的四条边是无法算出它的面积的。

例如说，你有四根一样长的棍子首尾相连拼成一个正方形，接着，你捏着它两头拉开，变成一个菱形，它的四条边没有变，但是面积却变小了。

但是，我们也不是没有办法只知道四条边求四边形面积，但是这种四边形比较特殊。接下来隆重介绍——婆罗摩笈多公式！

婆罗摩笈多公式

圆内接四边形四边分别为 a,b,c,da,b,c,d，则该四边形面积为 (p−a)(p−b)(p−c)(p−d)\sqrt{(p-a)(p-b)(p-c)(p-d)}。其中，pp 为四边形的半周长，即 p=a+b+c+d2p=\dfrac{a+b+c+d}{2}。

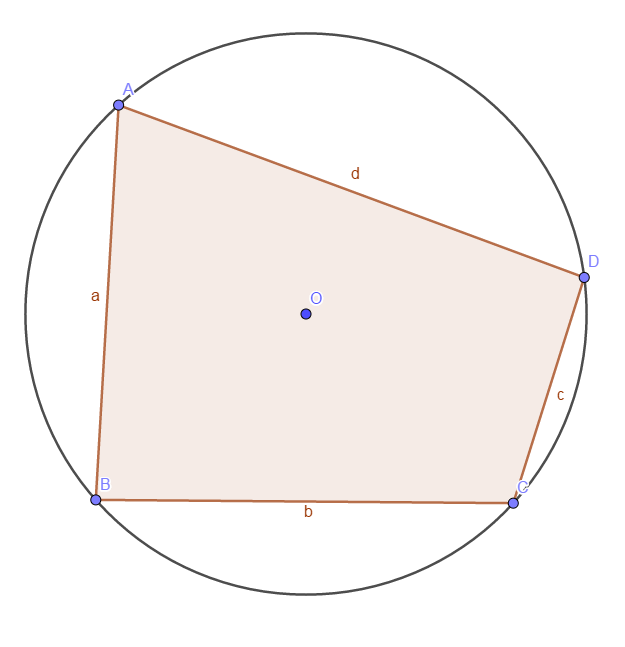
推导过程

我们先随便作一个外角，因为圆内接四边形对角互补，因此 ∠A=∠DCE\angle{A}=\angle{DCE}，然后我们连接对角线 BDBD，过 DD 分别作 DF⊥ABDF\perp AB，DG⊥BCDG\perp BC。设对角线 BD=gBD=g。

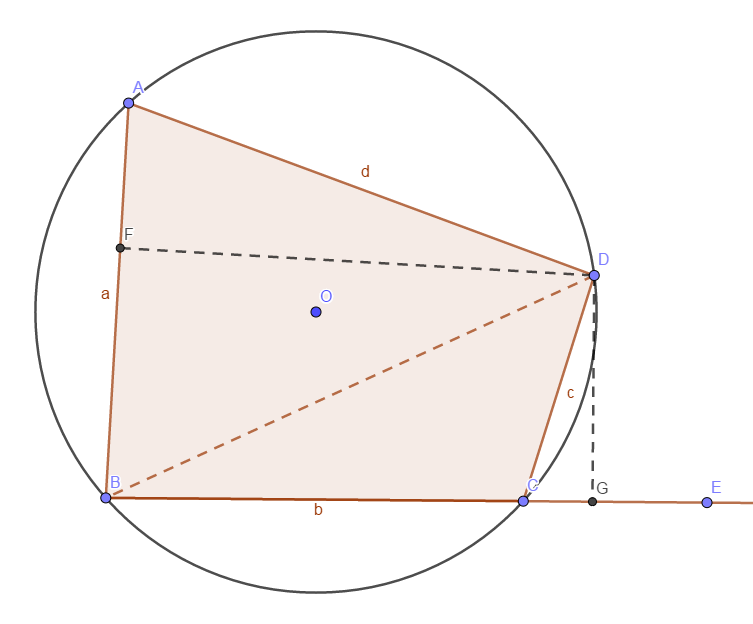
我们将焦点关注在 △ADB\triangle{ADB} 中，设 AF=xAF=x，则由勾股定理可得：

d2−x2=g2−(a−x)2d2−x2=g2−a2+2ax−x2x=a2+d2−g22a\begin{aligned} d^2-x^2&=g^2-{(a-x)}^2\\ d^2-x^2&=g^2-a^2+2ax-x^2\\ x&=\dfrac{a^2+d^2-g^2}{2a}\\ \end{aligned}

因此，sin⁡A=FDd=1dd2−(a2+d2−g22a)2\sin{A}=\dfrac{FD}{d}=\dfrac{1}{d}\sqrt{d^2-{\left(\dfrac{a^2+d^2-g^2}{2a}\right)}^2}。

同样地，关注 △DCB\triangle{DCB}，设 CG=yCG=y，则：

c2−y2=g2−(b+y)2c2−y2=g2−b2−2by−y2y=g2−b2−c22b\begin{aligned} c^2-y^2&=g^2-{(b+y)^2}\\ c^2-y^2&=g^2-b^2-2by-y^2\\ y&=\dfrac{g^2-b^2-c^2}{2b}\\ \end{aligned}

因此，sin⁡∠DCG=DGc=1cc2−(g2−b2−c22b)2\sin{\angle{DCG}}=\dfrac{DG}{c}=\dfrac{1}{c}\sqrt{c^2-{\left(\dfrac{g^2-b^2-c^2}{2b}\right)}^2}。

结合两个式子可以得到：

1dd2−(a2+d2−g22a)2=1cc2−(g2−b2−c22b)21−(a2+d2−g22ad)2=1−(g2−b2−c22bc)2a2+d2−g22ad=g2−b2−c22bca2+d22ad−g22ad=g22bc−b2+c22bcg22ad+g22bc=a2+d22ad+b2+c22bcbcg2+adg2=bc(a2+d2)+ad(b2+c2)g2=ad(b2+c2)+bc(a2+d2)ad+bc\begin{aligned} \dfrac{1}{d}\sqrt{d^2-{\left(\dfrac{a^2+d^2-g^2}{2a}\right)}^2}&=\dfrac{1}{c}\sqrt{c^2-{\left(\dfrac{g^2-b^2-c^2}{2b}\right)}^2}\\ \sqrt{1-{\left(\dfrac{a^2+d^2-g^2}{2ad}\right)}^2}&=\sqrt{1-{\left(\dfrac{g^2-b^2-c^2}{2bc}\right)}^2}\\ \dfrac{a^2+d^2-g^2}{2ad}&=\dfrac{g^2-b^2-c^2}{2bc}\\ \dfrac{a^2+d^2}{2ad}-\dfrac{g^2}{2ad}&=\dfrac{g^2}{2bc}-\dfrac{b^2+c^2}{2bc}\\ \dfrac{g^2}{2ad}+\dfrac{g^2}{2bc}&=\dfrac{a^2+d^2}{2ad}+\dfrac{b^2+c^2}{2bc}\\ bcg^2+adg^2&=bc(a^2+d^2)+ad(b^2+c^2)\\ g^2&=\dfrac{ad(b^2+c^2)+bc(a^2+d^2)}{ad+bc} \end{aligned}

当然，g2g^2 可以继续化简为 (ab+cd)(ac+bd)ad+bc\dfrac{(ab+cd)(ac+bd)}{ad+bc}，虽然长得挺好看，但是这不方便我们接下来的化简。

将其代回 sin⁡A=1dd2−(a2+d2−g22a)2\sin{A}=\dfrac{1}{d}\sqrt{d^2-{\left(\dfrac{a^2+d^2-g^2}{2a}\right)}^2} 中：

sin⁡A=1dd2−(a2+d2−g22a)2=1−(a2+d2−g22ad)2=1−(a2+d2−ad(b2+c2)+bc(a2+d2)ad+bc2ad)2=1−(a2(ad+bc)+d2(ad+bc)−ad(b2+c2)−bc(a2+d2)2ad(ad+bc))2=1−(ad(a2+d2)+bc(a2+d2)−ad(b2+c2)−bc(a2+d2)2ad(ad+bc))2=1−((a2+d2−b2−c2)2(ad+bc))2=(1+a2+d2−b2−c22(ad+bc))(1−a2+d2−b2−c22(ad+bc))=2ad+2bc+a2+d2−b2−c22(ad+bc)⋅2ad+2bc−a2−d2+b2+c22(ad+bc)=(a+d)2−(b−c)22(ad+bc)⋅(b+c)2−(a−d)22(ad+bc)=(a+d+b−c)(a+d−b+c)(b+c+a−d)(b+c−a+d)4(ad+bc)2\begin{aligned} \sin{A}&=\dfrac{1}{d}\sqrt{d^2-{\left(\dfrac{a^2+d^2-g^2}{2a}\right)}^2}\\ &=\sqrt{1-{\left(\dfrac{a^2+d^2-g^2}{2ad}\right)}^2}\\ &=\sqrt{1-{\left(\dfrac{a^2+d^2-\dfrac{ad(b^2+c^2)+bc(a^2+d^2)}{ad+bc}}{2ad}\right)}^2}\\ &=\sqrt{1-{\left(\dfrac{a^2(ad+bc)+d^2(ad+bc)-ad(b^2+c^2)-bc(a^2+d^2)}{2ad(ad+bc)}\right)}^2}\\ &=\sqrt{1-{\left(\dfrac{ad(a^2+d^2)+bc(a^2+d^2)-ad(b^2+c^2)-bc(a^2+d^2)}{2ad(ad+bc)}\right)}^2}\\ &=\sqrt{1-{\left(\dfrac{(a^2+d^2-b^2-c^2)}{2(ad+bc)}\right)}^2}\\ &=\sqrt{\left(1+\dfrac{a^2+d^2-b^2-c^2}{2(ad+bc)}\right)\left(1-\dfrac{a^2+d^2-b^2-c^2}{2(ad+bc)}\right)}\\ &=\sqrt{\dfrac{2ad+2bc+a^2+d^2-b^2-c^2}{2(ad+bc)}\cdot\dfrac{2ad+2bc-a^2-d^2+b^2+c^2}{2(ad+bc)}}\\ &=\sqrt{\dfrac{{(a+d)}^2-{(b-c)}^2}{2(ad+bc)}\cdot\dfrac{{(b+c)}^2-{(a-d)}^2}{2(ad+bc)}}\\ &=\sqrt{\dfrac{(a+d+b-c)(a+d-b+c)(b+c+a-d)(b+c-a+d)}{4{(ad+bc)}^2}}\\ \end{aligned}

因此，我们可以知道四边形的面积为：

S=a⋅DF2+b⋅DG2=a⋅sin⁡A⋅d+b⋅sin⁡∠DCG⋅c2=ad+bc2⋅sin⁡A=ad+bc2⋅(a+d+b−c)(a+d−b+c)(b+c+a−d)(b+c−a+d)4(ad+bc)2=(a+d+b−c)2(a+d−b+c)2(b+c+a−d)2(b+c−a+d)2=(p−a)(p−b)(p−c)(p−d)\begin{aligned} S&=\dfrac{a\cdot DF}{2}+\dfrac{b\cdot DG}{2}\\ &=\dfrac{a\cdot\sin{A}\cdot d+b\cdot\sin{\angle{DCG}}\cdot c}{2}\\ &=\dfrac{ad+bc}{2}\cdot\sin{A}\\ &=\dfrac{ad+bc}{2}\cdot\sqrt{\dfrac{(a+d+b-c)(a+d-b+c)(b+c+a-d)(b+c-a+d)}{4{(ad+bc)}^2}}\\ &=\sqrt{\dfrac{(a+d+b-c)}{2}\dfrac{(a+d-b+c)}{2}\dfrac{(b+c+a-d)}{2}\dfrac{(b+c-a+d)}{2}}\\ &=\sqrt{(p-a)(p-b)(p-c)(p-d)} \end{aligned}

即

S=(p−a)(p−b)(p−c)(p−d)S=\sqrt{(p-a)(p-b)(p-c)(p-d)}

拓展：圆的半径是多少？

这个也不复杂，我们连接 OCOC 和 ODOD，过 OO 作 OH⊥CDOH\perp CD。

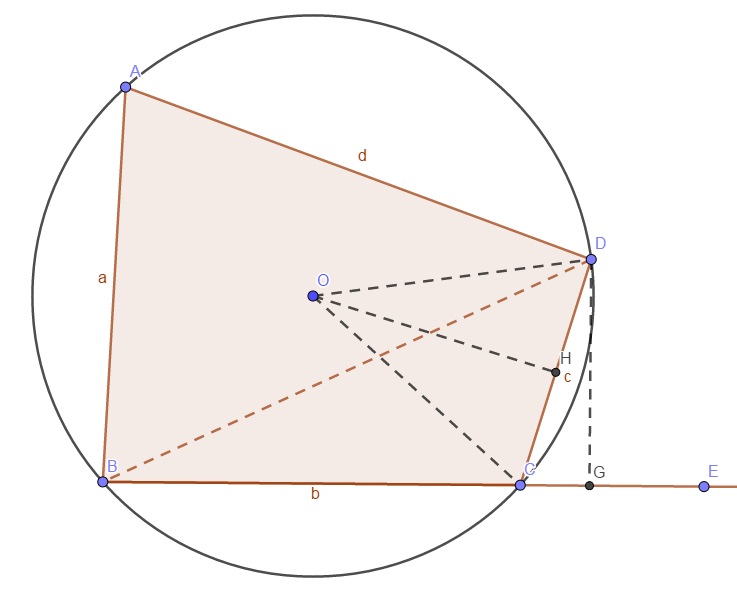
那么我们便有了一个「三线合一」，可以得到 DH=c2DH=\dfrac{c}{2}，∠DOH=12∠DOC=∠DBG\angle{DOH}=\dfrac12\angle{DOC}=\angle{DBG}。

抓住这两个角的相等关系，列出式子（RR 为圆的半径，SS 为四边形面积）：

sin⁡∠DOH=sin⁡∠DBGDHDO=DGDBc2R=sin⁡A⋅cgR=g2sin⁡AR=g22Sad+bcR=(ad+bc)g4SR=(ad+bc)(ab+cd)(ac+bd)ad+bc4SR=(ad+bc)(ab+cd)(ac+bd)4SR=(ad+bc)(ab+cd)(ac+bd)4(p−a)(p−b)(p−c)(p−d)R=14(ad+bc)(ab+cd)(ac+bd)(p−a)(p−b)(p−c)(p−d)\begin{aligned} \sin{\angle{DOH}}&=\sin{\angle{DBG}}\\ \dfrac{DH}{DO}&=\dfrac{DG}{DB}\\ \dfrac{c}{2R}&=\dfrac{\sin{A}\cdot c}{g}\\ R&=\dfrac{g}{2\sin{A}}\\ R&=\dfrac{g}{2\frac{2S}{ad+bc}}\\ R&=\dfrac{(ad+bc)g}{4S}\\ R&=\dfrac{(ad+bc)\sqrt{\dfrac{(ab+cd)(ac+bd)}{ad+bc}}}{4S}\\ R&=\dfrac{\sqrt{(ad+bc)(ab+cd)(ac+bd)}}{4S}\\ R&=\dfrac{\sqrt{(ad+bc)(ab+cd)(ac+bd)}}{4\sqrt{(p-a)(p-b)(p-c)(p-d)}}\\ R&=\dfrac14\sqrt{\dfrac{(ad+bc)(ab+cd)(ac+bd)}{(p-a)(p-b)(p-c)(p-d)}}\\ \end{aligned}

小结

若圆内接四边形四条边长分别为 a,b,c,da,b,c,d，则有以下结论（p=a+b+c+d2p=\dfrac{a+b+c+d}{2}）：

  • 四边形面积 S=(p−a)(p−b)(p−c)(p−d)S=\sqrt{(p-a)(p-b)(p-c)(p-d)}
  • 圆半径 R=14(ad+bc)(ab+cd)(ac+bd)(p−a)(p−b)(p−c)(p−d)R=\dfrac14\sqrt{\dfrac{(ad+bc)(ab+cd)(ac+bd)}{(p-a)(p-b)(p-c)(p-d)}}

本文中婆罗摩笈多公式的推导仅用了初中知识（三角函数，圆周角定理等），另外，配合正弦定理和余弦定理也可以推导出这几个公式。