wow，仔细一看，自己五个月没更新了呢！

这个问题的灵感来源于学校的数学卷中的某道数学题。

题目

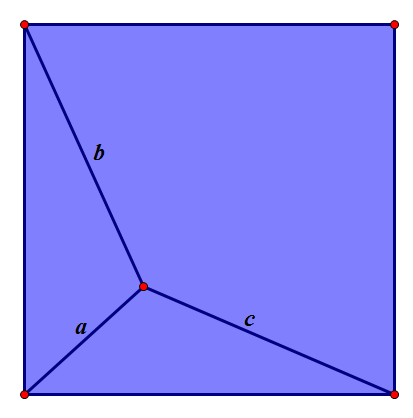
如图，已知正方形内有一点，连接其左下、左上、右下顶点，长度分别为 a,b,ca,b,c，求正方形的边长。

俩个余弦~

我们标好字母，借鉴原卷解法的思想，将左边的三角形顺时针旋转 90∘90^\circ（严谨点说，就是作 △CE′D\triangle CE'D 使其与 △CEA\triangle CEA 全等）。

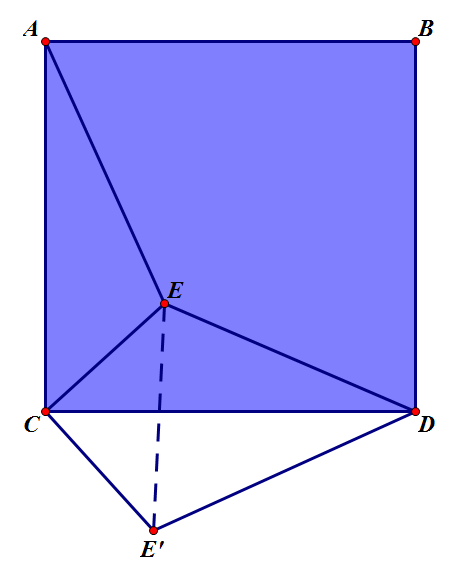
根据旋转不改变图形大小和形状的性质，我们可以知道下面几点，它对我们解题非常有帮助。

  1. △CEE′\triangle CEE' 为等腰直角三角形。
  2. DE′=AE=bDE'=AE=b。
  3. AE⊥DE′AE\perp DE'（这个很重要！我看了很久才发现有这条规律！）。

所以 EE′,BE,BE′EE',BE,BE' 分别等于 2a,c,b\sqrt2a,c,b。

利用两次余弦定理，得到答案：

cos⁡∠EE′D=2a2+b2−c222ab∠EE′D=cos⁡−1(2a2+b2−c222ab)⇓∠CE′D=∠EE′D+45∘=cos⁡−1(2a2+b2−c222ab)+45∘⇓再次使用余弦定理CD=a2+b2−2abcos⁡∠CE′D=a2+b2−2abcos⁡(cos⁡−1(2a2+b2−c222ab)+45∘)\begin{aligned} &\boxed{ \begin{aligned} \cos{\angle EE'D}&=\frac{2a^2+b^2-c^2}{2\sqrt2ab}\\ \angle EE'D&=\cos^{-1}\left(\frac{2a^2+b^2-c^2}{2\sqrt2ab}\right)\\ \end{aligned} }\\ &\qquad\qquad\qquad\qquad\Downarrow\\ &\boxed{ \begin{aligned} \angle CE'D&=\angle EE'D+45^\circ\\ &=\cos^{-1}\left(\frac{2a^2+b^2-c^2}{2\sqrt2ab}\right)+45^\circ\\ \end{aligned} }\\ &\qquad\qquad\qquad\qquad\Downarrow再次使用余弦定理\\ &\boxed{ \begin{aligned} CD&=\sqrt{a^2+b^2-2ab\cos\angle CE'D}\\ &=\sqrt{a^2+b^2-2ab\cos\left(\cos^{-1}\left(\frac{2a^2+b^2-c^2}{2\sqrt2ab}\right)+45^\circ\right)} \end{aligned} }\\ \end{aligned}

疯狂的勾股定理

​ 我没学过三角函数，所以这个表达式我不会化简，很丑陋（其实下面的那个公式似乎更加丑陋），而且日常使用比较难计算。所以我在想有没有其他的方法。我在宿舍床上想了很久，突然灵感就出来了，那时候直接跑出阳台借着灯光记了下来，然后心满意足的睡觉。如图，我们延长 AEAE 交 DE′DE' 于 FF：

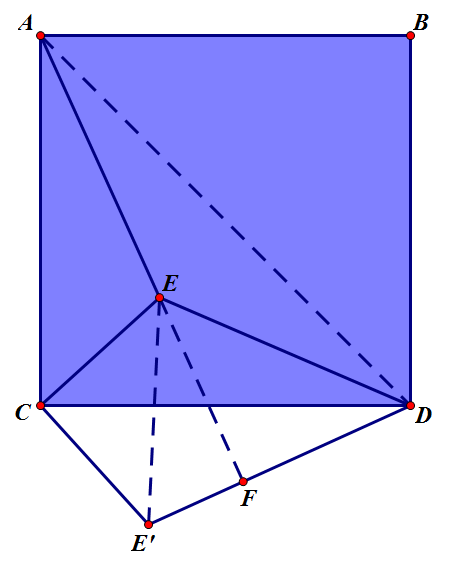
我们先来看 △EE′D\triangle EE'D，我们已经知道其三条边，并且我们知道AF⊥DE′AF\perp DE'，设 FD=xFD=x，利用勾股定理我们可以得到：

c2−x2=2a2−(b−x)2x=b2+c2−2a22b\begin{aligned} c^2-x^2&=2a^2-(b-x)^2\\ x&=\frac{b^2+c^2-2a^2}{2b} \end{aligned}

因此：

AD=AF2+x2=(b+c2−x2)2+x2=b2+c2+(2bc−b2−c2+2a2)(2bc+b2+c2−2a2)\begin{aligned} AD&=\sqrt{{AF}^2+x^2}\\ &=\sqrt{\left(b+\sqrt{c^2-x^2}\right)^2+x^2}\\ &=\sqrt{b^2+c^2+\sqrt{\left(2bc-b^2-c^2+2a^2\right)\left(2bc+b^2+c^2-2a^2\right)}} \end{aligned}

对角线来了，边长还会远吗？ AB=AD2AB=\frac{AD}{\sqrt2}，所以边长就等于：

b2+c22+14(2bc−b2−c2+2a2)(2bc+b2+c2−2a2)\sqrt{\frac{b^2+c^2}{2}+\sqrt{\frac14(2bc-b^2-c^2+2a^2)(2bc+b^2+c^2-2a^2)}}

如果你愿意，可以再变得美观一些（就是那个 2\sqrt2 有点丑了）：

b2+c22+14(2a+b+c)(2a+b−c)(2a+c−b)(b+c−2a)\sqrt{\frac{b^2+c^2}{2}+\sqrt{\frac14(\sqrt2a+b+c)(\sqrt2a+b-c)(\sqrt2a+c-b)(b+c-\sqrt2a)}}

再一种做法——解析几何

（为了方便阅读，我将常数 a,b,c\rm a,b,c 标为正体，变量 g,x,yg,x,y 标为斜体）

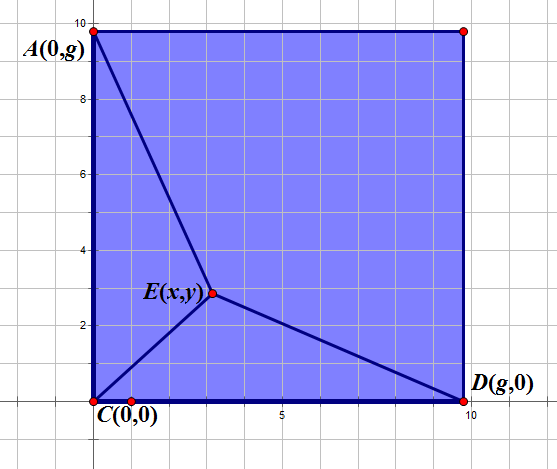
如图，我们可以得到一个三元二次方程组：

{CE:x2+y2=a2…(1)AE:x2+(g−y)2=b2…(2)DE:(g−x)2+yx=c2…(3)\left\{ \begin{aligned} CE:&&x^2+y^2=\rm a^2\dots(1)\\ AE:&&x^2+{(g-y)}^2=\rm b^2\dots(2)\\ DE:&&{(g-x)}^2+y^x=\rm c^2\dots(3)\\ \end{aligned} \right.

(2)−(1)(2)-(1) 得到 y=g2+a2−b22gy=\dfrac{g^2+{\rm a^2-b^2}}{2g}；(3)−(1)(3)-(1) 得到 x=g2+a2−c22gx=\dfrac{g^2+{\rm a^2-c^2}}{2g}。

将 xx 和 yy 代入 (1)(1)，得到：

(g2+a2−c22g)2+(g2+a2−b22g)2=a2{\left(\dfrac{g^2+{\rm a^2-c^2}}{2g}\right)}^2+{\left(\dfrac{g^2+{\rm a^2-b^2}}{2g}\right)}^2=\rm a^2

解得：

g=±b2+c22±14(2a+b+c)(2a+b−c)(2a+c−b)(b+c−2a)g=\rm\pm\sqrt{\frac{b^2+c^2}{2}\pm\sqrt{\frac14(\sqrt2a+b+c)(\sqrt2a+b-c)(\sqrt2a+c-b)(b+c-\sqrt2a)}}

去掉多余的根，得到：

g=b2+c22+14(2a+b+c)(2a+b−c)(2a+c−b)(b+c−2a)g=\rm\sqrt{\frac{b^2+c^2}{2}+\sqrt{\frac14(\sqrt2a+b+c)(\sqrt2a+b-c)(\sqrt2a+c-b)(b+c-\sqrt2a)}}

由海伦公式引出的推论

根据海伦公式，其实可以变换成一个更简洁的公式：

b2+c22+2S△EE′D\sqrt{\frac{b^2+c^2}{2}+2S_{\triangle EE'D}}

因为 b2+c22\frac{b^2+c^2}{2} 实质上是以 bb 和 cc 为直角边的等腰直角三角形的面积和，所以我们就可以得到：

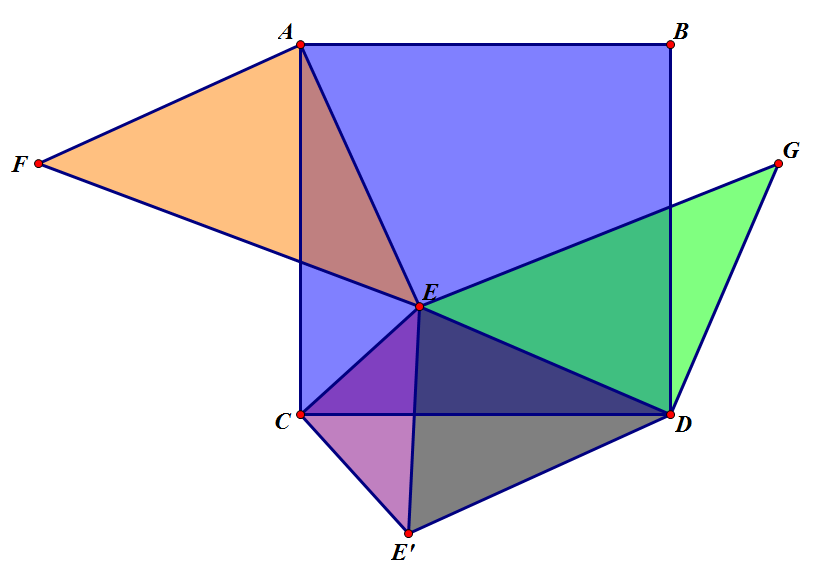
SABCD=S△AEF+S△DEG+2S△DEE′S_{ABCD}=S_{\triangle AEF}+S_{\triangle DEG}+2S_{\triangle DEE'}

这可能是这个图形中有关结论中最简洁的一个了吧。

从正四边形到正三边形

同样地，如果把正方形换成等边三角形，通过类似的方法，也可以求出边长。

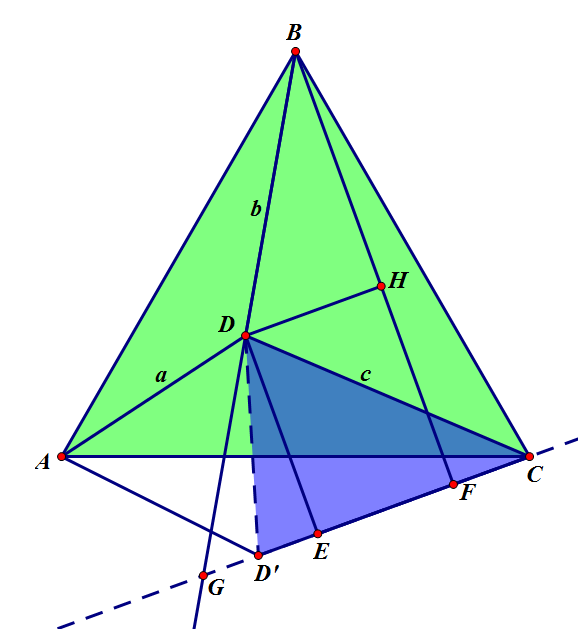
如图，方法还是旋转，突破点还是旋转角度 ∠BGC=60∘\angle BGC=60^\circ。

再作几条垂线，用勾股定理就可以求出 BCBC 的长度。

方法不再赘述，这里放上公式，推出来的朋友可以对一下答案：

a2+b2+c22+34(a+b+c)(a+b−c)(a+c−b)(b+c−a)\sqrt{\frac{a^2+b^2+c^2}{2}+\sqrt{\frac{3}{4}(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}