前几天看《可怕的科学——特别要命的数学》看到一章《吉帕特的大轮回》十分有意思，简直是表白神器！！

先来玩个小游戏

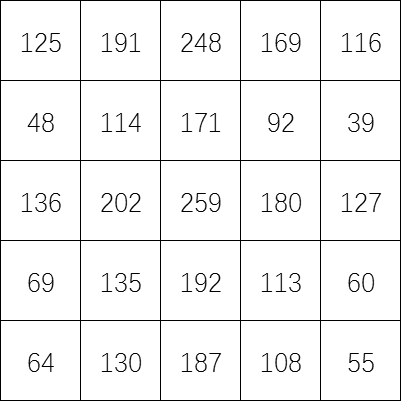
这是一块「魔板」，我们按下面操作：

1. 选一个白色格子，把它涂成蓝色，并把这个格子同行列的格子涂成红色。

2. 在剩下的白色格子里重复执行上面的操作，直到你涂了 5 个格子为止。

3. 把蓝色格子里的数加起来，你会发现答案总是 666！

例如如下：

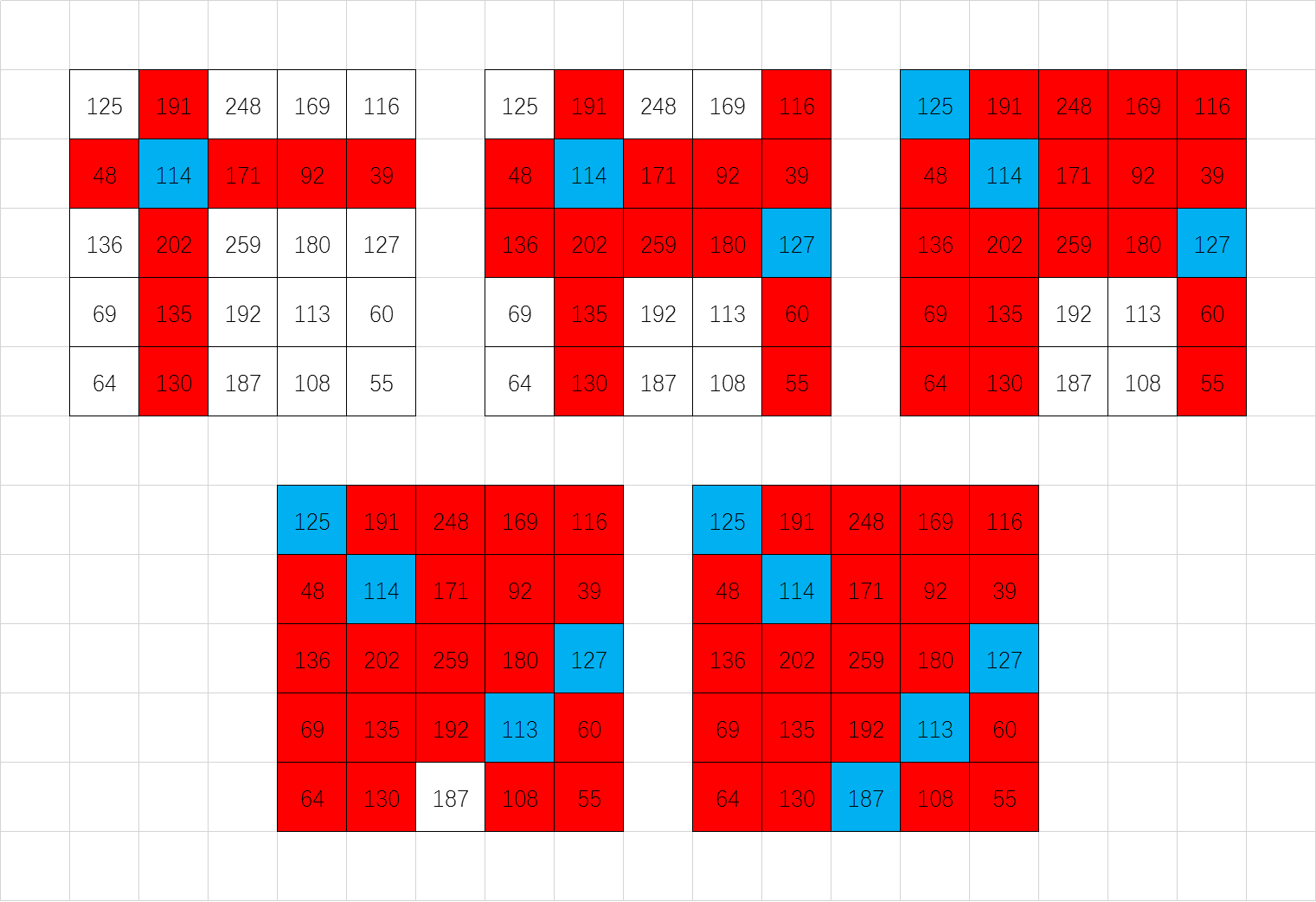
通过上图我们可以得出 $114+127+125+113+187=666$！

如何打造一个爆款魔板

1. 先画好一个 $5\times 5$ 的表格。

2. 选择一个你想要的结果 $x$（就如上面的 666）。这里我使用 $x=520$。

3. 选择九个正整数使它们的和等于 $x$。我这里随便选了 $1+2+3+4+50+99+112+119+130=520$。

4. 在这九个数之间选择其中五个数填在表格的某一列，并将它亲切地称为「固定列」。

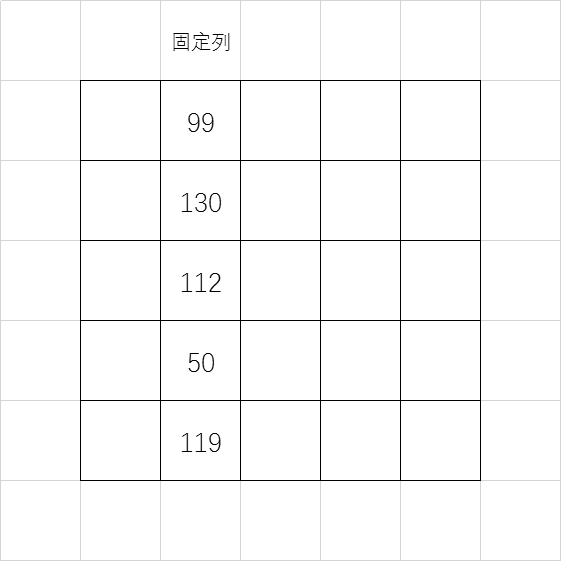
5. 在剩下的四列中，在每一列顶端随机写下剩下的四个正整数（不是填进格子里，写在表格的上面），这个数字称为这一列的「幸运数字」。

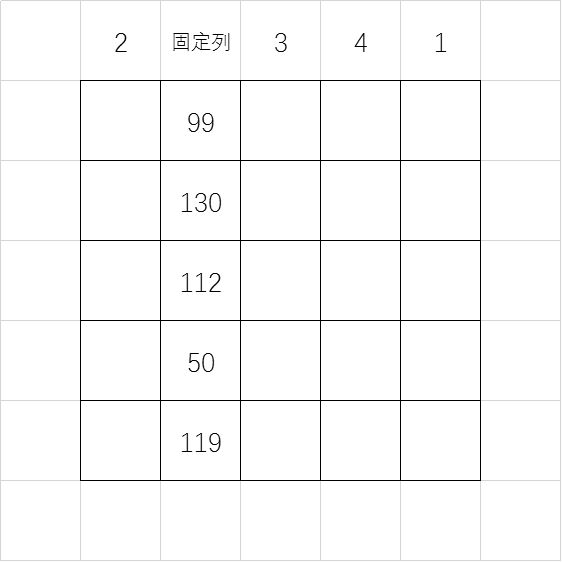
6. 对于剩下的 20 个格子：等于这个格子所在的一列的「幸运数字」加上这个格子所在一行的与「固定列」相交的格子里的数。

   例如左上角的格子所在的一列的「幸运数字」是 2 ，所在一行的与「固定列」相交的格子里的数是 99，那么左上角这个格子就是 $2+99=101$。

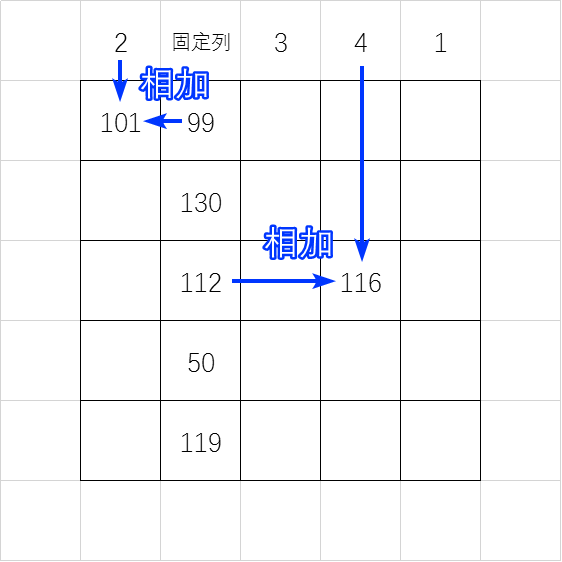
7. 以此类推，我们可以得到下面这个表格：

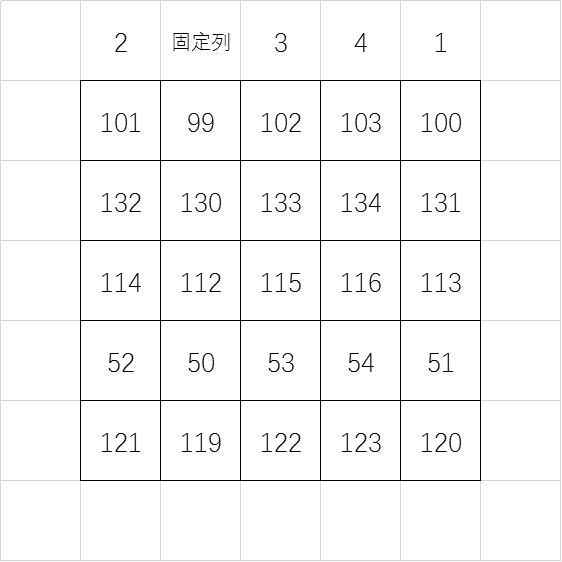
8. 别忘了把你的「幸运数字」擦掉避免被人发现。

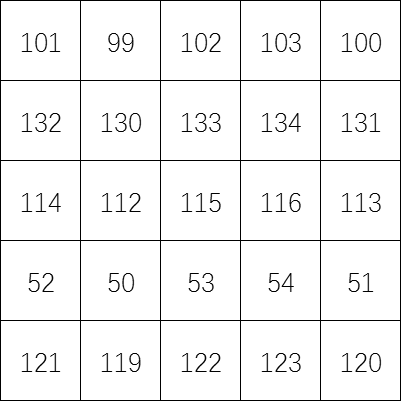
这样，表格就完成了。

这是什么原理？

​ 首先，你有没有发现关键的一点：

涂蓝色的五个格子一定互不同行不同列。

​ 因为我们每选完一个格子，我们就把它同行同列的格子涂成红色了，因此我们就不能选与它同行同列的格子了，因此这五个格子一定互不同行不同列。回到这张图：

因为只有五列五列，因此被选中的格子也有五个，他们还不同行同列，那么每行每列有且仅有一个被选中的格子。又因为每个格子是同行同列的「幸运数字」和「固定列」上的数字的和（「固定列」上的「幸运数字」可以看做是 0）。那么你能否想到，每个「固定列」上的数字有且仅有一次被加到结果里，而且「幸运数字」也是有且仅有一次被加到结果里？

如果你不能想到，那也别急，我们可以这样想：

• 对于每个「幸运数字」来说，如果有一个蓝色格子被选到在它的这一列，那么就给答案加上这个「幸运数字」。

• 同样的，对于每个「固定列」上的数字来说，如果有一个蓝色格子被选到在它的这一行，那么就给答案加上这个数字。

• 因为我们刚刚说那么每行每列有且仅有一个涂蓝色的格子，那么每个「幸运数字」和「固定列」上的数有且仅有一次被加到结果里。

• 那么答案就是每个「幸运数字」和「固定列」上的数的总和，也就是你想要的数字。

而为什么要选择九个正整数的原因也昭然若揭了：

因为能让每行每列都能都能只被选中一次。

更 多 玩 法

如果你已经掌握了原理，你就能制作出无数个这样的表格。如果你比较聪明，你就还找到更多玩法：

1. 表格不一定是$5\times 5$的正方形，可以是$n\times n$的正方形，只不过记住制作时是选择 $(2n-1)$ 个数的总和成为你的结果。

2. 你所选择的那九个数也不一定是正整数，可以是任何实数！

3. 做好后可以把魔板里的数字旋转、翻转或者扔进油锅里炸一炸。