​ 很显然，我失踪了很久，大概快有两年了吧。

​ 这两年里，第一年是初三，第二年是高一。第一年是备战中考，第二年是投身竞赛。

​ 事实上，我建立博客几乎纯粹是因为初二疫情，在家里闲着没事做。回校后，基本只有周末能回家，很少写博客，最多在学校搞搞研究（其实也很少），然后发出来（请见 用初中知识推导婆罗摩笈多公式 一文）。一上高中，我去了数学竞赛组。学业繁重，一个月回家一天，对于我这种迫切回家放松自我的人来说，不可能花时间写博客。

​ 但是，塞翁失马焉知非福。当我上了高中，却有实实在在地感受到了自己在数学方面的进步，以下是我挤时间写的一些感悟。

回首过去

​ 当我回看自己之前写的文章时，很多之前不能解决的问题都能迎刃而解，这大概是高中数学学习和竞赛学习带给我的吧。

​ 高中之前，我对三角函数的认知只停留在对边比斜边 、正余弦定理和反三角函数。学了三角恒等变换后，利用公式 $\cos{(\alpha+\beta)}=\cos\alpha\cos\beta-\sin\alpha\sin\beta$ 和 $\sin^2\alpha+\cos^2\alpha=1$ 很容易可以把 你能求出正方形的边长吗？ 一文中的余弦套反余弦式子化简。

​ 进了数学竞赛组后，我对数学有了更加深刻的理解和学习。如果将 “复杂”的相遇问题 一文中最后的幂级数公式中的 $g$ 换成关于 $x$ 的函数 $g(x)$，那么 $g(x)=\dfrac{1}{1-x}$ 就是数列 $[1,1,1,1,\cdots]$ 的母函数（生成函数）。这是一个非常强大的数列处理工具，可以用于推导数列通项或无穷级数求和。

​ 在竞赛组里，我也学习了高斯函数（取整函数） $\lfloor x\rfloor$，因此 魔术背后的 1.618 一文中我曾经不会解的奇怪方程利用高斯函数的定义可以轻松解决。那时，我趁热打铁，又研究了一下这个问题，收获颇丰，晚些再将成果补上（挖坑挖坑）。

​ 在文章 x^a+yb=z^c 的求解 中，通解也可以用中国剩余定理（孙子定理）得出，这也是我去了数学竞赛后不定方程的学习成果。有趣的是，我们教练甚至在课上出了一模一样的题目，于是我上去潇洒地在黑板写下了答案。事后，教练又抛出一个问题：方程的所有解都符合通解吗？当然教练本身也不知道答案。我回家利用 python 枚举，发现还有其他的解：

${9375}^3+{625}^4={250}^5$

​ 还记得初中时有一次做有关燕尾定理的题目时发现了这个结论：

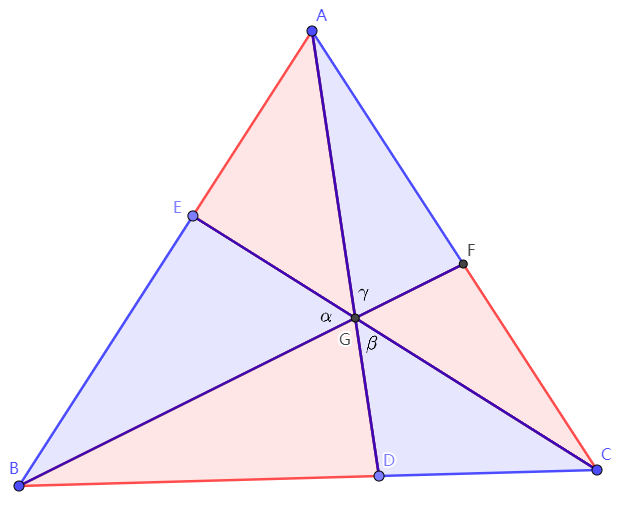
若AD,BF,CE三线共点，则三个红色三角形面积之积等于三个蓝色三角形面积之积。

​ 证明是简单的，利用三角形面积公式 $S=\dfrac{1}{2}ab\sin{C}$ 可以知道三个红色三角形面积之积和三个蓝色三角形面积之积均等于 $\dfrac18GA\cdot GB\cdot GC\cdot GD\cdot GE\cdot GF\cdot\sin\alpha\sin\beta\sin\gamma$。事实上，将其变形令等号一边为 1，再利用面积比等于底的比就可以得到竞赛平面几何中常用的塞瓦(Ceva)定理：

$\dfrac{AE}{EB}\cdot\dfrac{BD}{DC}\cdot\dfrac{CF}{FA}=1$

展望将来

​ 大概是要等到大学才能发表大量博客文章了，高中的话我可能最多写一些数学竞赛的学习笔记或者一些随笔发表到博客上。高中主要有这么几个计划：

• 挤时间学完高等数学和离散数学的内容，入门一些线性代数的内容，虽然这些对数学竞赛没有多大帮助但是就当课外阅读了。
• 硬肝初等数论。
• 先把文化课搞好，然后再专心致志搞数学竞赛！

​ 祝我成功 😃